Introdução
Os logaritmos foram inventados para acelerar e simplificar os cálculos. A ideia de logaritmo, ou seja, a ideia de expressar números como potências da mesma base, pertence a Mikhail Stiefel. Mas na época de Stiefel a matemática não estava tão desenvolvida e a ideia do logaritmo não estava desenvolvida. Os logaritmos foram posteriormente inventados simultânea e independentemente um do outro pelo cientista escocês John Napier (1550-1617) e pelo suíço Jobst Burgi (1552-1632). Napier foi o primeiro a publicar o trabalho em 1614. intitulado "Descrição da incrível tabela de logaritmos", a teoria dos logaritmos de Napier foi apresentada com detalhes suficientes na íntegra, o método de cálculo dos logaritmos é o mais simples, portanto os méritos de Napier na invenção dos logaritmos são maiores que os de Bürgi. Bürgi trabalhou nas mesas ao mesmo tempo que Napier, mas por muito tempo manteve-os em segredo e publicou-os apenas em 1620. Napier dominou a ideia do logaritmo por volta de 1594. embora as tabelas tenham sido publicadas 20 anos depois. A princípio ele chamou seus logaritmos de “números artificiais” e só então propôs chamar esses “números artificiais” em uma palavra de “logaritmo”, que traduzido do grego significa “números correlacionados”, tirado um de uma progressão aritmética e o outro de uma progressão geométrica especialmente selecionada para isso. As primeiras tabelas em russo foram publicadas em 1703. com a participação de um maravilhoso professor do século XVIII. L. F. Magnitsky. No desenvolvimento da teoria dos logaritmos ótimo valor teve os trabalhos do acadêmico de São Petersburgo Leonhard Euler. Ele foi o primeiro a considerar os logaritmos como o inverso da elevação a uma potência; ele introduziu os termos “base do logaritmo” e “mantissa”. Briggs compilou tabelas de logaritmos com base 10. As tabelas decimais são mais convenientes para uso prático, sua teoria é. mais simples que os logaritmos de Napier. Portanto, os logaritmos decimais às vezes são chamados de logaritmos de Briggs. O termo "caracterização" foi introduzido por Briggs.
Naqueles tempos distantes, quando os sábios começaram a pensar em igualdades contendo quantidades desconhecidas, provavelmente não existiam moedas ou carteiras. Mas havia pilhas, assim como potes e cestos, perfeitos para o papel de esconderijos que podiam conter um número desconhecido de itens. Nos antigos problemas matemáticos da Mesopotâmia, Índia, China, Grécia, quantidades desconhecidas expressavam o número de pavões no jardim, o número de touros no rebanho e a totalidade das coisas levadas em conta na divisão da propriedade. Escribas, funcionários e sacerdotes iniciados no conhecimento secreto, bem treinados na ciência da contabilidade, lidaram com tais tarefas com bastante sucesso.
Fontes que chegaram até nós indicam que os cientistas antigos possuíam algumas técnicas gerais para resolver problemas com quantidades desconhecidas. No entanto, nem um único papiro ou tabuinha de argila contém uma descrição dessas técnicas. Os autores apenas ocasionalmente forneciam aos seus cálculos numéricos comentários acanhados como: “Olha!”, “Faça isto!”, “Você encontrou o caminho certo”. Nesse sentido, a exceção é a “Aritmética” do matemático grego Diofante de Alexandria (século III) - uma coleção de problemas para a composição de equações com apresentação sistemática de suas soluções.
No entanto, o primeiro manual para resolução de problemas que se tornou amplamente conhecido foi o trabalho do cientista de Bagdá do século IX. Muhammad bin Musa al-Khwarizmi. A palavra "al-jabr" do nome árabe deste tratado - "Kitab al-jaber wal-mukabala" ("Livro de restauração e oposição") - acabou se transformando na conhecida palavra "álgebra", e al- O próprio trabalho de Khwarizmi serviu de ponto de partida para o desenvolvimento da ciência da resolução de equações.
Equações logarítmicas e desigualdades
1. Equações logarítmicas
Uma equação contendo uma incógnita sob o sinal do logaritmo ou em sua base é chamada de equação logarítmica.
A equação logarítmica mais simples é uma equação da forma
registro um x = b . (1)
Declaração 1. Se um > 0, um≠ 1, equação (1) para qualquer real b tem uma solução única x = um b .
Exemplo 1. Resolva as equações:
a) registro 2 x= 3, b) log 3 x= -1,c)
Solução. Usando a afirmação 1, obtemos a) x= 2 3 ou x= 8; b) x= 3 -1 ou x= 1/3; c)
ou x = 1.Vamos apresentar as propriedades básicas do logaritmo.
P1. Identidade logarítmica básica:
Onde um > 0, um≠ 1 e b > 0.
P2. Logaritmo do produto de fatores positivos igual à soma logaritmos desses fatores:
registro um N 1 · N 2 = registro um N 1 + registro um N 2 (um > 0, um ≠ 1, N 1 > 0, N 2 > 0).
Comentário. Se N 1 · N 2 > 0, então a propriedade P2 assume a forma
registro um N 1 · N 2 = registro um |N 1 | + registro um |N 2 | (um > 0, um ≠ 1, N 1 · N 2 > 0).
P3. O logaritmo do quociente de dois números positivos é igual à diferença entre os logaritmos do dividendo e do divisor
Comentário. Se
, (que é equivalente N 1 N 2 > 0) então a propriedade P3 assume a formaP4. O logaritmo da potência de um número positivo é igual ao produto do expoente e o logaritmo deste número:
registro um N k = k registro um N (um > 0, um ≠ 1, N > 0).
Comentário. Se k- número par ( k = 2é), Que
registro um N 2é = 2é registro um |N | (um > 0, um ≠ 1, N ≠ 0).
P5. Fórmula para mudar para outra base:
em particular se N = b, obtemos
(um > 0, um ≠ 1, b > 0, b ≠ 1). (2)Usando as propriedades P4 e P5, é fácil obter seguintes propriedades
e, se em (5) c- número par ( c = 2n), ocorre
Vamos listar as principais propriedades da função logarítmica f (x) = registro um x :
1. O domínio de definição de uma função logarítmica é o conjunto dos números positivos.
2. O intervalo de valores da função logarítmica é um conjunto números reais.
3. Quando um> 1 função logarítmica é estritamente crescente (0< x 1 < x 2log um x 1 < logum x 2) e em 0< um < 1, - строго убывает (0 < x 1 < x 2log um x 1 > registro um x 2).
4. registro um 1 = 0 e log um um = 1 (um > 0, um ≠ 1).
5. Se um> 1, então a função logarítmica é negativa quando x(0;1) e positivo em x(1;+∞), e se 0< um < 1, то логарифмическая функция положительна при x (0;1) e negativo em x (1;+∞).
6. Se um> 1, então a função logarítmica é convexa para cima, e se um(0;1) - convexo para baixo.
As seguintes afirmações (ver, por exemplo) são usadas ao resolver equações logarítmicas.
Você acha que ainda dá tempo antes do Exame Estadual Unificado e você terá tempo para se preparar? Talvez seja assim. Mas, em qualquer caso, quanto mais cedo o aluno começar a se preparar, mais sucesso ele terá nos exames. Hoje decidimos dedicar um artigo às desigualdades logarítmicas. Esta é uma das tarefas, o que significa uma oportunidade de obter crédito extra.
Você já sabe o que é um logaritmo? Nós realmente esperamos que sim. Mas mesmo que você não tenha uma resposta para essa pergunta, não há problema. Entender o que é um logaritmo é muito simples.

Por que 4? Você precisa elevar o número 3 a esta potência para obter 81. Depois de compreender o princípio, você pode prosseguir para cálculos mais complexos.
Você passou por desigualdades há alguns anos. E desde então você os encontrou constantemente na matemática. Se você tiver problemas para resolver desigualdades, consulte a seção apropriada.
Agora que nos familiarizamos com os conceitos individualmente, vamos considerá-los em geral.
A desigualdade logarítmica mais simples.

As desigualdades logarítmicas mais simples não se limitam a este exemplo, existem mais três, apenas com sinais diferentes; Por que isso é necessário? Para entender melhor como resolver desigualdades com logaritmos. Agora vamos dar um exemplo mais aplicável, ainda bastante simples. Deixaremos as desigualdades logarítmicas complexas para mais tarde.

Como resolver isso? Tudo começa com ODZ. Vale a pena saber mais sobre isso se você quiser resolver qualquer desigualdade sempre com facilidade.
O que é ODZ? ODZ para desigualdades logarítmicas
A abreviatura significa a faixa de valores aceitáveis. Essa formulação costuma surgir nas tarefas do Exame de Estado Unificado. ODZ será útil para você não apenas no caso de desigualdades logarítmicas.
Veja novamente o exemplo acima. Consideraremos o ODZ com base nele, para que você entenda o princípio, e resolver desigualdades logarítmicas não levante dúvidas. Da definição de logaritmo segue-se que 2x+4 deve ser maior que zero. No nosso caso, isso significa o seguinte.

Este número, por definição, deve ser positivo. Resolva a desigualdade apresentada acima. Isso pode até ser feito oralmente; aqui fica claro que X não pode ser menor que 2. A solução para a desigualdade será a definição da faixa de valores aceitáveis.
Agora, vamos resolver a desigualdade logarítmica mais simples.

Descartamos os próprios logaritmos de ambos os lados da desigualdade. O que nos resta como resultado? Desigualdade simples.

Não é difícil de resolver. X deve ser maior que -0,5. Agora combinamos os dois valores obtidos em um sistema. Por isso,

Esta será a faixa de valores aceitáveis para a desigualdade logarítmica em consideração.
Por que precisamos de ODZ? Esta é uma oportunidade para eliminar respostas incorretas e impossíveis. Se a resposta não estiver dentro da faixa de valores aceitáveis, então a resposta simplesmente não faz sentido. Vale a pena lembrar por muito tempo, pois no Exame Estadual Unificado muitas vezes há necessidade de busca por ODZ, e isso não se aplica apenas a desigualdades logarítmicas.
Algoritmo para resolver a desigualdade logarítmica
A solução consiste em várias etapas. Primeiro, você precisa encontrar o intervalo de valores aceitáveis. Haverá dois significados na ODZ, discutimos isso acima. Em seguida, você precisa resolver a própria desigualdade. Os métodos de solução são os seguintes:
- método de substituição de multiplicador;
- decomposição;
- método de racionalização.
Dependendo da situação, vale a pena usar um dos métodos acima. Vamos diretamente para a solução. Vamos revelar o método mais popular, adequado para resolver tarefas do Exame de Estado Unificado em quase todos os casos. A seguir veremos o método de decomposição. Pode ajudar se você se deparar com uma desigualdade particularmente complicada. Então, um algoritmo para resolver a desigualdade logarítmica.
Exemplos de soluções :

Não é à toa que pegamos exatamente essa desigualdade! Preste atenção na base. Lembre-se: se for maior que um, o sinal permanece o mesmo ao encontrar a faixa de valores aceitáveis; caso contrário, você precisará alterar o sinal de desigualdade.
Como resultado, obtemos a desigualdade:

Agora reduzimos o lado esquerdo à forma da equação igual a zero. Em vez do sinal “menor que” colocamos “igual” e resolvemos a equação. Assim, encontraremos o ODZ. Esperamos que você não tenha problemas para resolver uma equação tão simples. As respostas são -4 e -2. Isso não é tudo. Você precisa exibir esses pontos no gráfico, colocando “+” e “-”. O que precisa ser feito para isso? Substitua os números dos intervalos na expressão. Onde os valores são positivos, colocamos “+” ali.
Responder: x não pode ser maior que -4 e menor que -2.
Encontramos o intervalo de valores aceitáveis apenas para o lado esquerdo, agora precisamos encontrar o intervalo de valores aceitáveis para o lado direito. Isso é muito mais fácil. Resposta: -2. Cruzamos ambas as áreas resultantes.
E só agora começamos a abordar a própria desigualdade.

Vamos simplificar ao máximo para facilitar a solução.

Novamente usamos o método de intervalo na solução. Vamos pular os cálculos; tudo já está claro no exemplo anterior. Responder.

Mas este método é adequado se a desigualdade logarítmica tiver as mesmas bases.
Resolvendo equações logarítmicas e desigualdades com por diferentes razões pressupõe uma redução inicial a uma base. Em seguida, use o método descrito acima. Mas há mais caso difícil. Vamos considerar um dos mais espécies complexas desigualdades logarítmicas.
Desigualdades logarítmicas com base variável
Como resolver desigualdades com tais características? Sim, e essas pessoas podem ser encontradas no Exame de Estado Unificado. Resolver as desigualdades da seguinte forma também beneficiará o seu processo educacional. Vejamos a questão em detalhes. Vamos descartar a teoria e ir direto para a prática. Para resolver desigualdades logarítmicas, basta ler o exemplo uma vez.

Para resolver uma desigualdade logarítmica da forma apresentada, é necessário reduzir o lado direito a um logaritmo de mesma base. O princípio se assemelha a transições equivalentes. Como resultado, a desigualdade ficará assim.

Na verdade, resta apenas criar um sistema de desigualdades sem logaritmos. Usando o método de racionalização, passamos para um sistema equivalente de desigualdades. Você entenderá a regra em si quando substituir os valores apropriados e acompanhar suas alterações. O sistema terá as seguintes desigualdades.

Ao usar o método de racionalização ao resolver desigualdades, é preciso lembrar o seguinte: um deve ser subtraído da base, x, por definição do logaritmo, é subtraído de ambos os lados da desigualdade (direita da esquerda), duas expressões são multiplicadas e definido sob o sinal original em relação a zero.
A solução adicional é realizada pelo método intervalar, tudo é simples aqui. É importante que você entenda as diferenças nos métodos de solução, então tudo começará a funcionar facilmente.
Existem muitas nuances nas desigualdades logarítmicas. Os mais simples deles são bastante fáceis de resolver. Como você pode resolver cada um deles sem problemas? Você já recebeu todas as respostas neste artigo. Agora você tem uma longa prática pela frente. Pratique constantemente a resolução de uma variedade de problemas no exame e você poderá obter a pontuação mais alta. Boa sorte para você em sua difícil tarefa!
Entre toda a variedade de desigualdades logarítmicas, as desigualdades com base variável são estudadas separadamente. Eles são resolvidos usando uma fórmula especial, que por algum motivo raramente é ensinada na escola:
log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) - g (x)) (k (x) - 1) ∨ 0
Em vez da caixa de seleção “∨”, você pode colocar qualquer sinal de desigualdade: mais ou menos. O principal é que em ambas as desigualdades os sinais são iguais.
Desta forma, eliminamos os logaritmos e reduzimos o problema a uma desigualdade racional. Este último é muito mais fácil de resolver, mas ao descartar logaritmos, podem aparecer raízes extras. Para eliminá-los, basta encontrar a faixa de valores aceitáveis. Se você esqueceu o ODZ de um logaritmo, recomendo fortemente repeti-lo - veja “O que é um logaritmo”.
Tudo relacionado à faixa de valores aceitáveis deve ser anotado e resolvido separadamente:
f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.
Estas quatro desigualdades constituem um sistema e devem ser satisfeitas simultaneamente. Quando o intervalo de valores aceitáveis for encontrado, resta cruzá-lo com a solução da desigualdade racional - e a resposta está pronta.
Tarefa. Resolva a desigualdade:
Primeiro, vamos escrever o ODZ do logaritmo:
As duas primeiras desigualdades são satisfeitas automaticamente, mas a última deverá ser escrita. Como o quadrado de um número é zero se e somente se o próprio número for zero, temos:
x 2 + 1 ≠ 1;
x2 ≠ 0;
x ≠ 0.
Acontece que o ODZ do logaritmo é composto por todos os números, exceto zero: x ∈ (−∞ 0)∪(0; +∞). Agora resolvemos a desigualdade principal:

Fazemos a transição da desigualdade logarítmica para a racional. A desigualdade original tem um sinal “menor que”, o que significa que a desigualdade resultante também deve ter um sinal “menor que”. Nós temos:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x) · (3 + x) · x 2< 0.
Os zeros desta expressão são: x = 3; x = −3; x = 0. Além disso, x = 0 é raiz da segunda multiplicidade, o que significa que ao passar por ela o sinal da função não muda. Nós temos:

Obtemos x ∈ (−∞ −3)∪(3; +∞). Este conjunto está totalmente contido no ODZ do logaritmo, o que significa que esta é a resposta.
Convertendo desigualdades logarítmicas
Freqüentemente, a desigualdade original é diferente da acima. Isso pode ser facilmente corrigido usando as regras padrão para trabalhar com logaritmos - consulte “Propriedades básicas dos logaritmos”. Nomeadamente:
- Qualquer número pode ser representado como um logaritmo com uma determinada base;
- A soma e a diferença de logaritmos com as mesmas bases podem ser substituídas por um logaritmo.
Separadamente, gostaria de lembrá-lo sobre a faixa de valores aceitáveis. Como pode haver vários logaritmos na desigualdade original, é necessário encontrar o VA de cada um deles. Por isso, esquema geral soluções para desigualdades logarítmicas são as seguintes:
- Encontre o VA de cada logaritmo incluído na desigualdade;
- Reduza a desigualdade a uma desigualdade padrão usando fórmulas para adicionar e subtrair logaritmos;
- Resolva a desigualdade resultante usando o esquema fornecido acima.
Tarefa. Resolva a desigualdade:
Vamos encontrar o domínio de definição (DO) do primeiro logaritmo:
Resolvemos usando o método de intervalo. Encontrando os zeros do numerador:
3x − 2 = 0;
x = 2/3.
Então - os zeros do denominador:
x − 1 = 0;
x = 1.
Marcamos zeros e sinais na seta de coordenadas:

Obtemos x ∈ (−∞ 2/3)∪(1; +∞). O segundo logaritmo terá o mesmo VA. Se você não acredita em mim, você pode verificar. Agora transformamos o segundo logaritmo para que a base seja dois:
Como você pode ver, os três na base e na frente do logaritmo foram reduzidos. Temos dois logaritmos com a mesma base. Vamos adicioná-los:

log 2 (x - 1) 2< 2;
log 2 (x - 1) 2< log 2 2 2 .
Obtivemos a desigualdade logarítmica padrão. Eliminamos os logaritmos usando a fórmula. Como a desigualdade original contém um sinal “menor que”, o resultado expressão racional também deve ser menor que zero. Nós temos:
(f (x) - g (x)) (k (x) - 1)< 0;
((x − 1) 2 − 2 2)(2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).
Temos dois conjuntos:
- ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
- Resposta do candidato: x ∈ (−1; 3).
Resta cruzar esses conjuntos - obtemos a resposta real:

Estamos interessados na intersecção de conjuntos, por isso selecionamos intervalos sombreados em ambas as setas. Obtemos x ∈ (−1; 2/3)∪(1; 3) - todos os pontos são perfurados.
Desigualdades logarítmicas
Nas lições anteriores conhecemos as equações logarítmicas e agora sabemos o que são e como resolvê-las. A lição de hoje será dedicada ao estudo das desigualdades logarítmicas. Quais são essas desigualdades e qual é a diferença entre resolver uma equação logarítmica e uma desigualdade?
Desigualdades logarítmicas são desigualdades que possuem uma variável aparecendo sob o sinal do logaritmo ou em sua base.
Ou também podemos dizer que uma desigualdade logarítmica é uma desigualdade em que o seu valor desconhecido, como numa equação logarítmica, aparecerá sob o sinal do logaritmo.
As desigualdades logarítmicas mais simples têm a seguinte forma:
onde f(x) e g(x) são algumas expressões que dependem de x.
Vejamos isso usando este exemplo: f(x)=1+2x+x2, g(x)=3x−1.
Resolvendo desigualdades logarítmicas
Antes de resolver desigualdades logarítmicas, é importante notar que quando resolvidas elas são semelhantes a desigualdades exponenciais, a saber:
Primeiro, ao passar de logaritmos para expressões sob o sinal de logaritmo, também precisamos comparar a base do logaritmo com um;
Em segundo lugar, ao resolver uma desigualdade logarítmica utilizando uma mudança de variáveis, precisamos resolver as desigualdades em relação à mudança até obtermos a desigualdade mais simples.
Mas você e eu consideramos aspectos semelhantes da resolução de desigualdades logarítmicas. Agora vamos prestar atenção a uma diferença bastante significativa. Você e eu sabemos que a função logarítmica tem um domínio de definição limitado, portanto, ao passar de logaritmos para expressões sob o sinal de logaritmo, precisamos levar em consideração a faixa de valores permitidos (ADV).
Ou seja, deve-se levar em consideração que ao resolver uma equação logarítmica, podemos primeiro encontrar as raízes da equação e depois verificar esta solução. Mas resolver uma desigualdade logarítmica não funcionará desta forma, pois ao passar dos logaritmos para expressões sob o sinal do logaritmo, será necessário anotar o ODZ da desigualdade.
Além disso, vale lembrar que a teoria das desigualdades consiste em números reais, que são positivos e números negativos, bem como o número 0.
Por exemplo, quando o número “a” é positivo, então você precisa usar a seguinte notação: a >0. Nesse caso, tanto a soma quanto o produto desses números também serão positivos.
O princípio básico para resolver uma desigualdade é substituí-la por uma desigualdade mais simples, mas o principal é que seja equivalente à dada. Além disso, também obtivemos uma desigualdade e a substituímos novamente por uma de forma mais simples, etc.
Ao resolver desigualdades com uma variável, você precisa encontrar todas as suas soluções. Se duas desigualdades têm a mesma variável x, então tais desigualdades são equivalentes, desde que suas soluções coincidam.
Ao realizar tarefas de resolução de desigualdades logarítmicas, deve-se lembrar que quando a > 1, então a função logarítmica aumenta, e quando 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Métodos para resolver desigualdades logarítmicas
Agora vamos dar uma olhada em alguns dos métodos que ocorrem na resolução de desigualdades logarítmicas. Para melhor compreensão e assimilação, tentaremos compreendê-los através de exemplos específicos.
Todos sabemos que a desigualdade logarítmica mais simples tem a seguinte forma:
Nesta desigualdade, V – é um dos seguintes sinais de desigualdade:<,>, ≤ ou ≥.
Quando a base de um determinado logaritmo é maior que um (a>1), fazendo a transição dos logaritmos para expressões sob o sinal do logaritmo, então nesta versão o sinal da desigualdade é preservado, e a desigualdade terá a seguinte forma:
que é equivalente a este sistema:

No caso em que a base do logaritmo é maior que zero e menor que um (0 Isso é equivalente a este sistema: Vejamos mais exemplos de resolução das desigualdades logarítmicas mais simples mostradas na imagem abaixo: Exercício. Vamos tentar resolver esta desigualdade: Resolvendo a faixa de valores aceitáveis. Agora vamos tentar multiplicar seu lado direito por: Vamos ver o que podemos descobrir: Agora, vamos prosseguir para a conversão de expressões sublogarítmicas. Devido ao fato de a base do logaritmo ser 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; E daí segue-se que o intervalo que obtivemos pertence inteiramente à ODZ e é uma solução para tal desigualdade. Aqui está a resposta que obtivemos: Agora vamos tentar analisar o que precisamos para resolver com sucesso as desigualdades logarítmicas. Primeiramente, concentre toda a sua atenção e procure não cometer erros ao realizar as transformações que se dão nesta desigualdade. Além disso, deve-se lembrar que ao resolver tais desigualdades, é necessário evitar expansões e contrações das desigualdades, o que pode levar à perda ou aquisição de soluções estranhas. Em segundo lugar, ao resolver desigualdades logarítmicas, você precisa aprender a pensar logicamente e compreender a diferença entre conceitos como um sistema de desigualdades e um conjunto de desigualdades, para que possa selecionar facilmente soluções para a desigualdade, enquanto é guiado por sua DL. Em terceiro lugar, para resolver com sucesso tais desigualdades, cada um de vocês deve conhecer perfeitamente todas as propriedades das funções elementares e compreender claramente o seu significado. Tais funções incluem não apenas logarítmicas, mas também racionais, de potência, trigonométricas, etc., em uma palavra, todas aquelas que você estudou durante a álgebra escolar. Como você pode ver, tendo estudado o tema das desigualdades logarítmicas, não há nada difícil em resolver essas desigualdades, desde que você seja cuidadoso e persistente no alcance de seus objetivos. Para evitar problemas na resolução de desigualdades, é necessário praticar o máximo possível, resolvendo vários problemas e ao mesmo tempo lembrar os métodos básicos de resolução de tais desigualdades e seus sistemas. Se você não conseguir resolver as desigualdades logarítmicas, deverá analisar cuidadosamente seus erros para não voltar a eles no futuro. Para entender melhor o tema e consolidar o material abordado, resolva as seguintes desigualdades: Definição de logaritmo A maneira mais fácil de escrevê-lo matematicamente é: A definição de logaritmo pode ser escrita de outra forma: Preste atenção às restrições impostas na base do logaritmo ( um) e para a expressão sublogarítmica ( x). No futuro, essas condições se transformarão em restrições importantes para OD, que deverão ser levadas em consideração na resolução de qualquer equação com logaritmos. Assim, agora, além das condições padrão que levam a restrições ao ODZ (positividade das expressões sob as raízes das potências pares, denominador diferente de zero, etc.), as seguintes condições também devem ser levadas em consideração: Observe que nem a base do logaritmo nem a expressão sublogarítmica podem ser iguais a zero. Observe também que o próprio valor do logaritmo pode assumir todos os valores possíveis, ou seja, O logaritmo pode ser positivo, negativo ou zero. Os logaritmos têm muitas propriedades diferentes que decorrem das propriedades das potências e da definição de um logaritmo. Vamos listá-los. Então, as propriedades dos logaritmos: Logaritmo do produto: Logaritmo de uma fração: Tirando o grau do sinal do logaritmo: Preste especial atenção àquelas das últimas propriedades listadas nas quais o sinal do módulo aparece após o grau ser obtido. Não se esqueça que ao colocar uma potência par fora do sinal do logaritmo, abaixo do logaritmo ou na base, deve-se deixar o sinal do módulo. Outras propriedades úteis dos logaritmos: A última propriedade é frequentemente usada em equações e desigualdades logarítmicas complexas. Ele deveria ser lembrado assim como todos os outros, embora muitas vezes seja esquecido. As equações logarítmicas mais simples são assim: E sua solução é dada por uma fórmula que segue diretamente da definição do logaritmo: Outras equações logarítmicas mais simples são aquelas que, usando transformações algébricas e as fórmulas e propriedades dos logaritmos acima, podem ser reduzidas à forma: A solução para tais equações levando em consideração a ODZ é a seguinte: Alguns outros equações logarítmicas com uma variável na base pode ser reduzido à forma: Nessas equações logarítmicas, a forma geral da solução também segue diretamente da definição do logaritmo. Somente neste caso existem restrições adicionais para DZ que precisam ser levadas em consideração. Como resultado, para resolver uma equação logarítmica com uma variável na base, é necessário resolver o seguinte sistema: Ao resolver equações logarítmicas mais complexas que não podem ser reduzidas a uma das equações apresentadas acima, também é usado ativamente método de substituição de variável. Como de costume, ao usar este método, é preciso lembrar que após a introdução da substituição, a equação deve ser simplificada e não conter mais a antiga incógnita. Você também precisa se lembrar de realizar a substituição reversa de variáveis. Às vezes, ao resolver equações logarítmicas, você também precisa usar método gráfico. Este método consiste em construir gráficos de funções que estão nos lados esquerdo e direito da equação com a maior precisão possível em um plano de coordenadas e, em seguida, encontrar as coordenadas de seus pontos de interseção no desenho. As raízes obtidas desta forma devem ser verificadas por substituição na equação original. Ao resolver equações logarítmicas, muitas vezes também é útil método de agrupamento. Ao utilizar este método, o principal a lembrar é que: para que o produto de vários fatores seja igual a zero, é necessário que pelo menos um deles seja igual a zero, e o resto existia. Quando os fatores são logaritmos ou parênteses com logaritmos, e não apenas parênteses com variáveis como nas equações racionais, muitos erros podem ocorrer. Já os logaritmos possuem muitas restrições quanto à região onde existem. Ao decidir sistemas de equações logarítmicas na maioria das vezes você precisa usar o método de substituição ou o método de substituição de variável. Se houver tal possibilidade, então, ao resolver sistemas de equações logarítmicas, deve-se esforçar-se para garantir que cada uma das equações do sistema seja individualmente levada a uma forma em que seja possível fazer a transição de uma equação logarítmica para uma equação logarítmica. racional. As desigualdades logarítmicas mais simples são resolvidas aproximadamente da mesma maneira que equações semelhantes. Primeiro, usando transformações algébricas e as propriedades dos logaritmos, devemos tentar trazê-los para uma forma onde os logaritmos nos lados esquerdo e direito da desigualdade tenham as mesmas bases, ou seja, obtenha uma desigualdade da forma: Depois disso, é necessário passar para uma desigualdade racional, levando em consideração que esta transição deve ser realizada da seguinte forma: se a base do logaritmo for maior que um, então o sinal da desigualdade não precisa ser alterado, e se o a base do logaritmo for menor que um, então você precisa mudar o sinal da desigualdade para o oposto (isso significa mudar “menos” para “mais” ou vice-versa). Neste caso, não há necessidade de alterar os sinais de menos para mais, contornando as regras previamente aprendidas. Vamos escrever matematicamente o que obtemos como resultado dessa transição. Se a base for maior que um, obtemos: Se a base do logaritmo for menor que um, mudamos o sinal da desigualdade e obtemos o seguinte sistema: Como vemos, ao resolver desigualdades logarítmicas, como de costume, o ODZ também é levado em consideração (esta é a terceira condição nos sistemas acima). Além disso, neste caso é possível não exigir a positividade de ambas as expressões sublogarítmicas, mas sim exigir a positividade apenas da menor delas. Ao decidir desigualdades logarítmicas com uma variável na base logaritmo, é necessário considerar ambas as opções de forma independente (quando a base é menor que um e maior que um) e combinar as soluções desses casos em um conjunto. Ao mesmo tempo, não devemos esquecer o DL, ou seja, sobre o fato de que tanto a base quanto todas as expressões sublogarítmicas devem ser positivas. Assim, ao resolver uma desigualdade da forma: Obtemos o seguinte conjunto de sistemas: Desigualdades logarítmicas mais complexas também podem ser resolvidas usando mudanças de variáveis. Algumas outras desigualdades logarítmicas (como equações logarítmicas) requerem o procedimento de levar o logaritmo de ambos os lados da desigualdade ou equação para a mesma base para serem resolvidas. Portanto, ao realizar tal procedimento com desigualdades logarítmicas, há uma sutileza. Observe que ao levar logaritmos para uma base maior que um, o sinal de desigualdade não muda, mas se a base for menor que um, o sinal de desigualdade é invertido. Se uma desigualdade logarítmica não pode ser reduzida a uma racional ou resolvida por substituição, então, neste caso, deve-se usar método de intervalo generalizado, que é o seguinte: Para se preparar com sucesso para o CT em física e matemática, entre outras coisas, é necessário cumprir três condições mais importantes: A implementação bem sucedida, diligente e responsável destes três pontos permitirá que você apresente um excelente resultado no CT, o máximo que você é capaz. Se você acha que encontrou um erro em materiais educativos, então escreva sobre isso por e-mail. Você também pode relatar um bug para rede social(). Na carta, indique a disciplina (física ou matemática), o nome ou número do tema ou prova, o número do problema ou o local do texto (página) onde, na sua opinião, há erro. Descreva também qual é o erro suspeito. Sua carta não passará despercebida, o erro será corrigido ou você será explicado por que não é um erro.

Resolvendo exemplos
![]()



3x > 24;
x > 8. ![]()
O que é necessário para resolver desigualdades logarítmicas?
Trabalho de casa




![]()
![]()

![]()


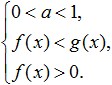

Como se preparar com sucesso para o CT em física e matemática?
Encontrou um erro?





