Voltar Avançar
Atenção! As visualizações de slides são apenas para fins informativos e podem não representar todos os recursos da apresentação. Se você estiver interessado neste trabalho, baixe a versão completa.
Objetivos da lição.
Educacional: Derive uma fórmula para calcular o volume de uma pirâmide
Desenvolvimento: desenvolver o interesse cognitivo dos alunos pelas disciplinas acadêmicas, a capacidade de aplicar seus conhecimentos na prática.
Educacional: cultivar a atenção, o rigor, ampliar os horizontes dos alunos.
Equipamentos e materiais: computador, tela, projetor, apresentação “Volume da Pirâmide”.
1. Levantamento frontal. Apresentações 2, 3
O que se chama pirâmide, base da pirâmide, costelas, altura, eixo, apótema. Qual pirâmide é chamada de pirâmide regular, tetraedro e truncada?
Uma pirâmide é um poliedro que consiste em uma superfície plana polígono, pontos, não estando no plano deste polígono e todos os segmentos, conectando este ponto com os pontos do polígono.
Este ponto chamado principal pirâmides, e um polígono plano é a base da pirâmide. Segmentos conectando o topo da pirâmide com os vértices da base são chamados costelas . Altura pirâmides - perpendicular, baixado do topo da pirâmide até o plano da base. Apótema - altura da borda lateral pirâmide correta. A pirâmide, que na base está correto n-gon, Um base de altura coincide com centro da base chamado correto pirâmide n-gonal. Eixo de uma pirâmide regular é a linha reta que contém sua altura. Uma pirâmide triangular regular é chamada de tetraedro. Se a pirâmide for interceptada por um plano paralelo ao plano da base, então ela cortará a pirâmide, semelhante dado. A parte restante é chamada pirâmide truncada.

2. Derivação da fórmula de cálculo do volume da pirâmide V=SH/3 Slides 4, 5, 6
1. Seja SABC uma pirâmide triangular com vértice S e base ABC.
2. Vamos adicionar esta pirâmide a um prisma triangular com a mesma base e altura.
3. Este prisma é composto por três pirâmides:
1) desta pirâmide SABC.
2) pirâmides SCC 1 B 1.
3) e pirâmides SCBB 1.
4. A segunda e a terceira pirâmides têm bases iguais CC 1 B 1 e B 1 BC e uma altura total traçada do vértice S até a face do paralelogramo BB 1 C 1 C. Portanto, elas têm volumes iguais.
5. A primeira e a terceira pirâmides também possuem bases SAB e BB 1 S iguais e alturas coincidentes traçadas do vértice C até a face do paralelogramo ABB 1 S. Portanto, também possuem volumes iguais.
Isso significa que todas as três pirâmides têm o mesmo volume. Como a soma desses volumes é igual ao volume do prisma, os volumes das pirâmides são iguais a SH/3.
O volume de qualquer pirâmide triangular é igual a um terço do produto da área da base pela altura.
3. Consolidação de novo material. Solução de exercícios.
1) Problema № 33 do livro de A.N. Pogorelova. Diapositivos 7, 8, 9
Do lado da base? e aresta lateral b, encontre o volume de uma pirâmide regular, na base da qual está:
1) triângulo,
2) quadrilátero,
3) hexágono.
Em uma pirâmide regular, a altura passa pelo centro do círculo circunscrito à base. Então: (Apêndice)
4. Informações históricas sobre as pirâmides. Diapositivos 15, 16, 17
O primeiro de nossos contemporâneos a estabelecer uma série de fenômenos incomuns associados à pirâmide foi o cientista francês Antoine Bovy. Ao explorar a pirâmide de Quéops na década de 30 do século XX, ele descobriu que os corpos de pequenos animais que acidentalmente acabavam na sala real eram mumificados. Bovey explicou a si mesmo a razão disso pelo formato de uma pirâmide e, como se viu, não se enganou. Seus trabalhos formaram a base da pesquisa moderna, como resultado, nos últimos 20 anos, surgiram muitos livros e publicações confirmando que a energia das pirâmides pode ter significado prático.
O Mistério das Pirâmides
Alguns pesquisadores argumentam que a pirâmide contém uma enorme quantidade de informações sobre a estrutura do Universo, do sistema solar e do homem, codificadas em sua forma geométrica, ou mais precisamente, na forma de um octaedro, metade do qual a pirâmide representa. A pirâmide com o topo para cima simboliza a vida, com o topo para baixo simboliza a morte. outro mundo. Assim como os componentes da Estrela de David (Magen David), onde um triângulo direcionado para cima simboliza a ascensão à Mente Superior, Deus, e um triângulo com o vértice para baixo simboliza a descida da alma à Terra, a existência material...
O valor digital do código com o qual as informações sobre o Universo são criptografadas na pirâmide, o número 365, não foi escolhido por acaso. Em primeiro lugar, este é o ciclo de vida anual do nosso planeta. Além disso, o número 365 é composto por três dígitos 3, 6 e 5. O que eles significam? Se em sistema solar O Sol passa no número 1, Mercúrio - 2, Vênus - 3, Terra - 4, Marte - 5, Júpiter - 6, Saturno - 7, Urano - 8, Netuno - 9, Plutão - 10, então 3 é Vênus, 6 - Júpiter e 5 - Marte. Conseqüentemente, a Terra está ligada de maneira especial a esses planetas. Somando os números 3, 6 e 5, obtemos 14, dos quais 1 é o Sol e 4 é a Terra.
O número 14 geralmente tem um significado global: em particular, a estrutura das mãos humanas é baseada nele, número total as falanges dos dedos de cada um também são 14. Este código também está relacionado à constelação da Ursa Maior, que inclui o nosso Sol, e na qual existiu outra estrela que destruiu Phaethon, um planeta localizado entre Marte e Júpiter, após o qual apareceu no sistema solar Plutão, e as características dos outros planetas mudaram.
Muitas fontes esotéricas afirmam que a humanidade na Terra já passou por quatro catástrofes mundiais. A terceira raça lemuriana conhecia a ciência divina do Universo, então esta doutrina secreta foi transmitida apenas aos iniciados. No início dos ciclos e meios ciclos do ano sideral, construíram pirâmides. Eles estavam perto de descobrir o código da vida. A civilização da Atlântida teve sucesso em muitas coisas, mas em algum nível de conhecimento foi interrompida por outra catástrofe planetária, acompanhada por uma mudança de raças. Provavelmente, os iniciados queriam nos transmitir que as pirâmides contêm conhecimento das leis cósmicas...
Dispositivos especiais na forma de pirâmides neutralizam a radiação eletromagnética negativa de um computador, TV, geladeira e outros eletrodomésticos elétricos em uma pessoa.
Um dos livros descreve um caso em que uma pirâmide instalada no habitáculo de um automóvel reduziu o consumo de combustível e reduziu o teor de CO nos gases de escape.
Sementes de culturas hortícolas mantidas em pirâmides tiveram melhor germinação e rendimento. As publicações até recomendavam embeber as sementes em água piramidal antes de semear.
Descobriu-se que as pirâmides têm um efeito benéfico no meio ambiente. Elimine zonas patogênicas em apartamentos, escritórios e chalés de verão, criando uma aura positiva.
O pesquisador holandês Paul Dickens, em seu livro, dá exemplos das propriedades curativas das pirâmides. Ele percebeu que com a ajuda deles é possível aliviar dores de cabeça, dores nas articulações, estancar sangramentos de pequenos cortes e que a energia das pirâmides estimula o metabolismo e fortalece o sistema imunológico.
Algumas publicações modernas observam que os medicamentos mantidos em pirâmide encurtam o curso do tratamento, e o curativo, saturado de energia positiva, promove a cicatrização de feridas.
Cremes e pomadas cosméticos melhoram seu efeito.
As bebidas, inclusive as alcoólicas, melhoram o sabor, e a água contida na vodca 40% torna-se curativa. Fiel à cobrança energia positiva para uma garrafa padrão de 0,5 litro, você precisará de uma pirâmide alta.
Uma matéria de jornal diz que se as joias forem guardadas sob uma pirâmide, elas se autolimpam e adquirem um brilho especial, e as pedras preciosas e semipreciosas acumulam bioenergia positiva e a liberam gradativamente.
Segundo cientistas americanos, produtos alimentícios como cereais, farinha, sal, açúcar, café, chá, depois de estarem na pirâmide, melhoram seu sabor e os cigarros baratos tornam-se semelhantes aos seus nobres irmãos.
Isso pode não ser relevante para muitos, mas em uma pequena pirâmide as velhas lâminas de barbear se afiam e em uma grande pirâmide a água não congela a -40 graus Celsius.
Segundo a maioria dos pesquisadores, tudo isso é prova da existência da energia piramidal.
Ao longo dos 5.000 anos de existência, as pirâmides tornaram-se uma espécie de símbolo, personificando o desejo do homem de alcançar o auge do conhecimento.
5. Resumindo a lição.
Lista de literatura usada.
1) http://schools.techno.ru
2) Pogorelov A.V. Geometria 10-11, editora Prosveshchenie.
3) Enciclopédia “Árvore do Conhecimento” Marshall K.
Metas e objetivos da aula:
- derivar fórmulas para o volume de uma pirâmide usando a fórmula básica para o volume dos corpos e o volume de uma pirâmide truncada.
- sistematizar conhecimentos teóricos sobre o tema da determinação do volume de uma pirâmide.
- desenvolver a habilidade de encontrar o volume de uma pirâmide cujo vértice é projetado no centro de um círculo inscrito ou circunscrito próximo à base.
- desenvolver habilidades na resolução de problemas padrão usando fórmulas para os volumes de uma pirâmide e de uma pirâmide truncada.
Progresso da lição
EU.Explicaçãomaterial novo.
A prova do teorema é realizada por meio de um projetor multimídia
Vamos provar o teorema: o volume da pirâmide éum terço, o produto da área da base pela altura.

Prova:
Primeiro provamos o teorema para uma pirâmide triangular, depois para uma arbitrária.
1. Considere uma pirâmide triangular OABC com volume V, área de base S e altura h. Vamos desenhar o eixo ah (OM 2- altura), considere a seção A 1 B 1 C 1 pirâmide com um plano perpendicular ao eixo Oh e, portanto, paralelo ao plano da base. Vamos denotar por X ponto de abscissa M 1
intersecção deste plano com o eixo x, e através S(x)- área da seção transversal. Vamos expressar S(x) através S, h E X. Observe que ![]()
De fato , por isso, .
Triângulos retos ![]() , também são semelhantes (eles têm um ângulo agudo comum com o vértice SOBRE).
, também são semelhantes (eles têm um ângulo agudo comum com o vértice SOBRE).

Apliquemos agora a fórmula básica para calcular os volumes dos corpos em um = 0, b =h nós conseguimos

2. Vamos agora provar o teorema para uma pirâmide arbitrária com altura h e área base S. Tal pirâmide pode ser dividida em pirâmides triangulares com altura total h. Vamos expressar o volume de cada pirâmide triangular usando a fórmula que provamos e adicionar esses volumes. Tirando o fator comum dos colchetes, obtemos entre colchetes a soma das bases das pirâmides triangulares, ou seja, área S das bases da pirâmide original.
Assim, o volume da pirâmide original é . O teorema foi provado.
II. resolver problemas usando desenhos prontos.

Tarefa 1. (Fig. 3)
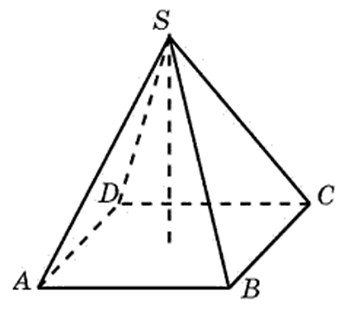
Dado:abcD- pirâmide regular AB = 3; ANÚNCIO = . Encontrar: UM) Sbásico; b) JSC; V) FAZER G) V .
Tarefa 2. (Fig. 4)
Dado:abcDF- pirâmide regular .
Tarefa 3. (Fig. 5)
Dado:abcDEKF- pirâmide regular
Encontrar: UM) Sbásico ; b) V.
Tarefa4. (fig.. 6)
Encontrar: V.
A verificação da tarefa é realizada através de um projetor multimídia com análise detalhada solução passo a passo.
Tarefa 1. (Fig. 3)
a) (a fórmula é usada para calcular a área de um triângulo regular)
AB = = 3, temos ![]()
b) ![]() (fórmula para o raio de um círculo circunscrito usando o lado de um triângulo equilátero)
(fórmula para o raio de um círculo circunscrito usando o lado de um triângulo equilátero) ![]() .
.

Tarefa 2. (Fig. 4)
1) Consideremos, portanto,
– isósceles, OS = FO = 2.

Tarefa 3. (Fig. 5)

Tarefa 4. (Fig. 6)

III. Verificando o resultado da fórmula de cálculo do volume de uma pirâmide truncada (a mensagem do aluno na lousa é feita por meio de um projetor multimídia)
Resposta do aluno:
Consideramos o volume de uma pirâmide truncada como a diferença de volumes pirâmide completa e aquele que dele é cortado por um plano paralelo à base (Fig. 1).


Vamos substituir esta expressão por X na primeira fórmula,

Trabalho em forma de teste, com verificação através de projetor multimídia.
1. Em um prisma inclinado, a aresta lateral tem 7 cm, a seção perpendicular é um triângulo retângulo com pernas: 4 cm e 3 cm.
a) 10 cm 3, b) 42 cm 3, c) 60 cm 3, d) 30 cm 3.
2. Da maneira certa pirâmide hexagonal O lado de sua base mede 2 cm. O volume da pirâmide é 6 cm3. Qual é a altura?

3. O volume da pirâmide é 56 cm 3, a área da base é 14 cm 2. Qual é a altura?
a) 14 cm, b) 12 cm, c) 16 cm.
4. Em uma pirâmide triangular regular, a altura é de 5 cm, os lados da base têm 3 cm. Qual é o volume da pirâmide?

5. Em uma pirâmide quadrangular regular, a altura é 9 cm. O lado da base mede 4 cm.
a) 50 cm 3, b) 48 cm 3, c) 16 cm 3.
6. O volume de uma pirâmide quadrangular regular é 27 cm 3, altura 9 cm.
a) 12 cm, b) 9 cm, c) 3 cm.
7. O volume de uma pirâmide truncada é 210 cm 3, a área da base inferior é 36 cm 2, a superior é 9 cm 2. Encontre a altura da pirâmide.
a) 1cm, b) 15cm, c) 10cm.
8. Um prisma de tamanho igual e uma pirâmide quadrangular regular têm alturas iguais. Qual é o lado da base da pirâmide se a área da base do prisma é S?

Tabela de respostas.
| Tarefa | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Responder | b | UM | b | UM | b | V | V | V |
Lição de casa: 1. Resolva os problemas nº 695v, nº 697, nº 690
2. Considere tarefas básicas
Tarefa 1.
Prove que se as arestas laterais da pirâmide são iguais (ou fazem ângulos iguais com o plano da base), então o topo da pirâmide é projetado no centro do círculo circunscrito à base.

Prove que se os ângulos diédricos na base da pirâmide são iguais (ou iguais às alturas das faces laterais desenhadas a partir do vértice da pirâmide), então o vértice da pirâmide é projetado no centro do círculo inscrito no base da pirâmide.

Aqui veremos exemplos relacionados ao conceito de volume. Para resolver tais problemas, você precisa conhecer a fórmula do volume da pirâmide:

S
h – altura da pirâmide
A base pode ser qualquer polígono. Mas na maioria dos problemas do Exame de Estado Unificado, a condição geralmente diz respeito a pirâmides regulares. Deixe-me lembrá-lo de uma de suas propriedades:
O topo de uma pirâmide regular é projetado no centro de sua base
Observe a projeção das pirâmides regulares triangulares, quadrangulares e hexagonais (VISTA SUPERIOR):

Você pode fazer isso no blog, onde foram discutidos problemas relacionados à localização do volume de uma pirâmide.Vamos considerar as tarefas:
27087. Encontre o volume de uma pirâmide triangular regular cujos lados da base são iguais a 1 e cuja altura é igual à raiz de três.


S– área da base da pirâmide
h– altura da pirâmide
Vamos encontrar a área da base da pirâmide, este é um triângulo regular. Vamos usar a fórmula - a área de um triângulo é igual à metade do produto dos lados adjacentes pelo seno do ângulo entre eles, o que significa:


Resposta: 0,25
27088. Encontre a altura de uma pirâmide triangular regular cujos lados da base são iguais a 2 e cujo volume é igual à raiz de três.

Conceitos como a altura de uma pirâmide e as características de sua base são relacionados pela fórmula do volume:

S– área da base da pirâmide
h– altura da pirâmide
Conhecemos o volume em si, podemos encontrar a área da base, pois conhecemos os lados do triângulo, que é a base. Conhecendo os valores indicados, podemos encontrar facilmente a altura.
Para encontrar a área da base, usamos a fórmula - a área de um triângulo é igual à metade do produto dos lados adjacentes e o seno do ângulo entre eles, o que significa:

Assim, substituindo esses valores na fórmula do volume, podemos calcular a altura da pirâmide:

A altura é três.
Resposta: 3
27109. Em uma pirâmide quadrangular regular, a altura é 6, a aresta lateral é 10. Encontre seu volume.
O volume da pirâmide é calculado pela fórmula:
S– área da base da pirâmide
h– altura da pirâmide
Sabemos a altura. Você precisa encontrar a área da base. Deixe-me lembrá-lo de que o topo de uma pirâmide regular é projetado no centro de sua base. A base de uma pirâmide quadrangular regular é um quadrado. Podemos encontrar sua diagonal. Considere um triângulo retângulo (destacado em azul):

O segmento que liga o centro do quadrado ao ponto B é uma perna igual à metade da diagonal do quadrado. Podemos calcular esta perna usando o teorema de Pitágoras:
Isso significa BD = 16. Vamos calcular a área do quadrado usando a fórmula da área de um quadrilátero:

Por isso:
Assim, o volume da pirâmide é:

Resposta: 256
27178. Em uma pirâmide quadrangular regular, a altura é 12 e o volume é 200. Encontre a aresta lateral desta pirâmide.

A altura da pirâmide e seu volume são conhecidos, o que significa que podemos encontrar a área do quadrado, que é a base. Conhecendo a área de um quadrado, podemos encontrar sua diagonal. A seguir, considerando um triângulo retângulo usando o teorema de Pitágoras, calculamos a aresta lateral:

Vamos encontrar a área do quadrado (base da pirâmide):

Vamos calcular a diagonal do quadrado. Como sua área é 50, o lado será igual à raiz de cinquenta e segundo o teorema de Pitágoras:
O ponto O divide a diagonal BD ao meio, o que significa a perna do triângulo retângulo OB = 5.
Assim, podemos calcular a que é igual a aresta lateral da pirâmide:
Resposta: 13
245353. Encontre o volume da pirâmide mostrada na figura. Sua base é um polígono cujos lados adjacentes são perpendiculares e uma das arestas laterais é perpendicular ao plano da base e igual a 3.

Como já foi dito várias vezes, o volume da pirâmide é calculado pela fórmula:

S– área da base da pirâmide
h– altura da pirâmide
A aresta lateral perpendicular à base é igual a três, o que significa que a altura da pirâmide é três. A base da pirâmide é um polígono cuja área é igual a:
Por isso:

Resposta: 27
27086. A base da pirâmide é um retângulo com lados 3 e 4. Seu volume é 16. Encontre a altura desta pirâmide.
Isso é tudo. Boa sorte para você!
Atenciosamente, Alexander Krutitskikh.
P.S: Ficaria muito grato se você me falasse sobre o site nas redes sociais.
Uma das figuras tridimensionais mais simples é uma pirâmide triangular, pois consiste em menor número faces a partir das quais uma figura pode ser formada no espaço. Neste artigo veremos fórmulas que podem ser usadas para encontrar o volume de uma pirâmide regular triangular.
Pirâmide triangular
De acordo com definição geral uma pirâmide é um polígono, cujos vértices estão conectados a um ponto não localizado no plano deste polígono. Se este último for um triângulo, então toda a figura é chamada de pirâmide triangular.
A pirâmide em questão consiste em uma base (triângulo) e três faces laterais (triângulos). O ponto onde as três faces laterais estão conectadas é chamado de vértice da figura. A perpendicular deste vértice até a base é a altura da pirâmide. Se o ponto de intersecção da perpendicular com a base coincide com o ponto de intersecção das medianas do triângulo na base, então falamos de uma pirâmide regular. Caso contrário, ficará inclinado.
Como afirmado, a base de uma pirâmide triangular pode ser um triângulo tipo geral. No entanto, se for equilátero e a pirâmide em si for reta, então eles falam de uma figura tridimensional regular.
Qualquer pirâmide triangular possui 4 faces, 6 arestas e 4 vértices. Se os comprimentos de todas as arestas forem iguais, essa figura é chamada de tetraedro.
tipo geral
Antes de escrever uma pirâmide triangular regular, damos uma expressão para esta quantidade física para uma pirâmide de tipo geral. Esta expressão se parece com:
Aqui S o é a área da base, h é a altura da figura. Esta igualdade será válida para qualquer tipo de base poligonal de pirâmide, bem como para um cone. Se na base houver um triângulo com comprimento lateral a e altura h o abaixado sobre ele, então a fórmula do volume será escrita da seguinte forma:
Fórmulas para o volume de uma pirâmide triangular regular
Uma pirâmide triangular regular tem triângulo equilátero na base. Sabe-se que a altura deste triângulo está relacionada ao comprimento do seu lado pela igualdade:
Substituindo esta expressão na fórmula do volume de uma pirâmide triangular escrita no parágrafo anterior, obtemos:
V = 1/6*a*h o *h = √3/12*a 2 *h.
O volume de uma pirâmide regular de base triangular é função do comprimento do lado da base e da altura da figura.
Como qualquer polígono regular pode ser inscrito em um círculo, cujo raio determinará exclusivamente o comprimento do lado do polígono, então esta fórmula pode ser escrita em termos do raio correspondente r:
Esta fórmula pode ser facilmente obtida a partir da anterior, se levarmos em conta que o raio r do círculo circunscrito através do comprimento do lado a do triângulo é determinado pela expressão:
Problema de determinação do volume de um tetraedro
Mostraremos como usar as fórmulas acima ao resolver problemas geométricos específicos.
Sabe-se que um tetraedro tem um comprimento de aresta de 7 cm. Encontre o volume de um tetraedro-pirâmide triangular regular.
Lembre-se de que um tetraedro é regular quando todas as bases são iguais entre si. Para usar a fórmula do volume triangular, você precisa calcular duas quantidades:
- comprimento do lado do triângulo;
- altura da figura.
A primeira quantidade é conhecida pela declaração do problema:
Para determinar a altura, considere o valor mostrado na figura.

O triângulo marcado ABC é um triângulo retângulo, onde o ângulo ABC é 90 o. O lado AC é a hipotenusa e seu comprimento é a. Usando um raciocínio geométrico simples, podemos mostrar que o lado BC tem o comprimento:
Observe que o comprimento BC é o raio do círculo circunscrito ao triângulo.
h = AB = √(AC 2 - BC 2) = √(a 2 - a 2/3) = a*√(2/3).
Agora você pode substituir he a na fórmula correspondente para o volume:
V = √3/12*a 2 *a*√(2/3) = √2/12*a 3 .
Assim, obtivemos a fórmula do volume de um tetraedro. Percebe-se que o volume depende apenas do comprimento da borda. Se substituirmos o valor da condição do problema na expressão, obteremos a resposta:
V = √2/12*7 3 ≈ 40,42 cm3.
Se compararmos este valor com o volume de um cubo de mesma aresta, descobrimos que o volume do tetraedro é 8,5 vezes menor. Isto indica que o tetraedro é uma figura compacta que ocorre em algumas substâncias naturais. Por exemplo, a molécula de metano tem uma forma tetraédrica e cada átomo de carbono no diamante está conectado a quatro outros átomos para formar um tetraedro.

Problema da pirâmide homotética
Vamos resolver um curioso problema geométrico. Suponha que exista uma pirâmide triangular regular com um certo volume V 1. Quantas vezes o tamanho desta figura deve ser reduzido para se obter uma pirâmide homotética com volume três vezes menor que o original?

Vamos começar a resolver o problema escrevendo a fórmula da pirâmide regular original:
V 1 = √3/12*a 1 2 *h 1 .
Seja o volume da figura exigido pelas condições do problema obtido multiplicando seus parâmetros pelo coeficiente k. Nós temos:
V 2 = √3/12*k 2 *a 1 2 *k*h 1 = k 3 *V 1 .
Como a proporção dos volumes das figuras é conhecida pela condição, obtemos o valor do coeficiente k:
k = ∛(V 2 /V 1) = ∛(1/3) ≈ 0,693.
Observe que obteríamos um valor semelhante do coeficiente k para uma pirâmide de qualquer tipo, e não apenas para uma triangular regular.
Uma pirâmide é um poliedro com um polígono na base. Todas as faces, por sua vez, formam triângulos que convergem em um vértice. As pirâmides são triangulares, quadrangulares e assim por diante. Para determinar qual pirâmide está à sua frente, basta contar o número de ângulos de sua base. A definição de “altura de uma pirâmide” é frequentemente encontrada em problemas de geometria no currículo escolar. Neste artigo tentaremos considerar maneiras diferentes a localização dela.
Partes da pirâmide
Cada pirâmide consiste nos seguintes elementos:
- faces laterais, que possuem três cantos e convergem no ápice;
- o apótema representa a altura que desce do seu ápice;
- o topo da pirâmide é um ponto que conecta as costelas laterais, mas não fica no plano da base;
- a base é um polígono no qual o vértice não se encontra;
- a altura de uma pirâmide é um segmento que cruza o topo da pirâmide e forma um ângulo reto com sua base.
Como encontrar a altura de uma pirâmide se seu volume for conhecido

Através da fórmula V = (S*h)/3 (na fórmula V é o volume, S é a área da base, h é a altura da pirâmide) descobrimos que h = (3*V)/ S. Para consolidar o material, vamos resolver imediatamente o problema. A base triangular mede 50 cm 2 , enquanto seu volume é 125 cm 3 . A altura da pirâmide triangular é desconhecida, e é isso que precisamos de determinar. Tudo é simples aqui: inserimos os dados em nossa fórmula. Obtemos h = (3*125)/50 = 7,5 cm.
Como encontrar a altura de uma pirâmide se o comprimento da diagonal e suas arestas são conhecidos
Como lembramos, a altura da pirâmide forma um ângulo reto com sua base. Isso significa que a altura, a aresta e a metade da diagonal juntas formam muitos, é claro, lembram-se do teorema de Pitágoras. Conhecendo duas dimensões, não será difícil encontrar a terceira quantidade. Lembremos o conhecido teorema a² = b² + c², onde a é a hipotenusa e, no nosso caso, a aresta da pirâmide; b - a primeira perna ou metade da diagonal ec - respectivamente, a segunda perna, ou a altura da pirâmide. Desta fórmula c² = a² - b².
Agora o problema: em uma pirâmide regular a diagonal é de 20 cm, quando o comprimento da aresta é de 30 cm Você precisa encontrar a altura. Resolvemos: c² = 30² - 20² = 900-400 = 500. Portanto c = √ 500 = cerca de 22,4.
Como encontrar a altura de uma pirâmide truncada
É um polígono com seção transversal paralela à sua base. A altura de uma pirâmide truncada é o segmento que conecta suas duas bases. A altura pode ser encontrada para uma pirâmide regular se os comprimentos das diagonais de ambas as bases, bem como a borda da pirâmide, forem conhecidos. Seja a diagonal da base maior d1, enquanto a diagonal da base menor seja d2 e a aresta tenha comprimento l. Para encontrar a altura, você pode diminuir as alturas dos dois pontos superiores opostos do diagrama até sua base. Vemos que temos dois triângulos retângulos, tudo o que resta é determinar os comprimentos dos seus catetos. Para fazer isso, subtraia a menor da diagonal maior e divida por 2. Assim encontraremos uma perna: a = (d1-d2)/2. Depois disso, de acordo com o teorema de Pitágoras, tudo o que precisamos fazer é encontrar a segunda perna, que é a altura da pirâmide.

Agora vamos ver tudo isso na prática. Temos uma tarefa pela frente. Uma pirâmide truncada tem um quadrado na base, o comprimento diagonal da base maior é de 10 cm, enquanto a menor tem 6 cm e a aresta tem 4 cm. Primeiro, encontramos uma perna: a = (10-6)/2 = 2 cm Uma perna é igual a 2 cm e a hipotenusa é 4 cm. Acontece que a segunda perna ou altura será igual a 16-. 4 = 12, ou seja, h = √12 = cerca de 3,5 cm.





