Invoering
Logaritmen zijn uitgevonden om berekeningen te versnellen en te vereenvoudigen. Het idee van een logaritme, dat wil zeggen het idee om getallen uit te drukken als machten met hetzelfde grondtal, is van Mikhail Stiefel. Maar in de tijd van Stiefel was de wiskunde nog niet zo ontwikkeld en was het idee van de logaritme niet ontwikkeld. Logaritmen werden later gelijktijdig en onafhankelijk van elkaar uitgevonden door de Schotse wetenschapper John Napier (1550-1617) en de Zwitser Jobst Burgi (1552-1632) was de eerste die het werk publiceerde in 1614. getiteld "Beschrijving van de verbazingwekkende tabel met logaritmen", werd Napier's theorie van logaritmen in voldoende mate gegeven volledig, de methode voor het berekenen van logaritmen wordt de eenvoudigste gegeven, daarom zijn de verdiensten van Napier bij de uitvinding van logaritmen groter dan die van Bürgi. Bürgi werkte tegelijkertijd met Napier aan de tafels, maar voor een lange tijd hield ze geheim en publiceerde ze pas in 1620. Napier beheerste het idee van de logaritme rond 1594. hoewel de tabellen twintig jaar later werden gepubliceerd. Aanvankelijk noemde hij zijn logaritmen ‘kunstmatige getallen’ en pas daarna stelde hij voor om deze ‘kunstmatige getallen’ in één woord ‘logaritme’ te noemen, wat vanuit het Grieks ‘gecorreleerde getallen’ betekent, de ene ontleend aan een rekenkundige reeks en de andere aan een geometrische progressie die speciaal daarvoor is geselecteerd. De eerste tabellen in het Russisch werden in 1703 gepubliceerd. met de deelname van een geweldige leraar uit de 18e eeuw. L.F. Magnitsky. Bij de ontwikkeling van de theorie van logaritmen grote waarde had het werk van de Sint-Petersburgse academicus Leonhard Euler. Hij was de eerste die logaritmen beschouwde als het omgekeerde van het verheffen tot een macht; hij introduceerde de termen ‘logaritmebasis’ en ‘mantisse’. Briggs stelde tabellen van logaritmen samen met grondtal 10. Decimale tabellen zijn handiger voor praktisch gebruik, hun theorie is eenvoudiger dan die van de logaritmen van Napier. Daarom worden decimale logaritmen soms Briggs-logaritmen genoemd. De term "karakterisering" werd geïntroduceerd door Briggs.
In die verre tijden, toen de wijzen voor het eerst begonnen na te denken over gelijkheden die onbekende hoeveelheden bevatten, bestonden er waarschijnlijk geen munten of portefeuilles. Maar er waren hopen, maar ook potten en manden, die perfect geschikt waren voor de rol van opslagplaatsen die een onbekend aantal items konden bevatten. In de oude wiskundige problemen van Mesopotamië, India, China en Griekenland drukten onbekende grootheden het aantal pauwen in de tuin uit, het aantal stieren in de kudde en het geheel van zaken waarmee rekening werd gehouden bij de verdeling van eigendommen. Schriftgeleerden, functionarissen en priesters die waren ingewijd in geheime kennis en goed waren opgeleid in de wetenschap van de rekeningen, konden dergelijke taken met succes aan.
Bronnen die ons hebben bereikt, geven aan dat wetenschappers uit de oudheid over enkele algemene technieken beschikten om problemen met onbekende grootheden op te lossen. Geen enkel papyrus- of kleitablet bevat echter een beschrijving van deze technieken. Slechts af en toe voorzagen de auteurs hun numerieke berekeningen van karige opmerkingen als: “Kijk!”, “Doe dit!”, “Je hebt de juiste gevonden.” In deze zin is de uitzondering de 'Rekenkunde' van de Griekse wiskundige Diophantus van Alexandrië (III eeuw) - een verzameling problemen voor het opstellen van vergelijkingen met een systematische presentatie van hun oplossingen.
De eerste handleiding voor het oplossen van problemen die algemeen bekend werd, was echter het werk van de Bagdad-wetenschapper uit de 9e eeuw. Muhammad bin Musa al-Khwarizmi. Het woord ‘al-jabr’, afgeleid van de Arabische naam van deze verhandeling – ‘Kitab al-jaber wal-mukabala’ (‘Boek van herstel en oppositie’) – veranderde in de loop van de tijd in het bekende woord ‘algebra’, en al- Khwarizmi's werk zelf vormde het startpunt in de ontwikkeling van de wetenschap van het oplossen van vergelijkingen.
Logaritmische vergelijkingen en ongelijkheden
1. Logaritmische vergelijkingen
Een vergelijking die een onbekende bevat onder het logaritmeteken of aan de basis ervan, wordt een logaritmische vergelijking genoemd.
De eenvoudigste logaritmische vergelijking is een vergelijking van de vorm
loggen A X = B . (1)
Verklaring 1. Als A > 0, A≠ 1, vergelijking (1) voor elke reële waarde B heeft een unieke oplossing X = een b .
Voorbeeld 1. Los de vergelijkingen op:
a)logboek 2 X= 3, b) logboek 3 X= -1,c)
Oplossing. Met behulp van stelling 1 verkrijgen we a) X= 2 3 of X= 8; B) X= 3 -1 of X= 1/3; C)
of X = 1.Laten we de basiseigenschappen van de logaritme presenteren.
P1. Basis logaritmische identiteit:
Waar A > 0, A≠ 1 en B > 0.
P2. Logaritme van het product van positieve factoren gelijk aan de som logaritmen van deze factoren:
loggen A N 1 · N 2 = logboek A N 1 + logboek A N 2 (A > 0, A ≠ 1, N 1 > 0, N 2 > 0).
Opmerking. Als N 1 · N 2 > 0, dan heeft eigenschap P2 de vorm
loggen A N 1 · N 2 = logboek A |N 1 | + logboek A |N 2 | (A > 0, A ≠ 1, N 1 · N 2 > 0).
P3. De logaritme van het quotiënt van twee positieve getallen is gelijk aan het verschil tussen de logaritmes van het deeltal en de deler
Opmerking. Als
, (wat gelijkwaardig is N 1 N 2 > 0), dan heeft eigenschap P3 de vormP4. De logaritme van de macht van een positief getal is gelijk aan het product van de exponent en de logaritme van dit getal:
loggen A N k = k loggen A N (A > 0, A ≠ 1, N > 0).
Opmerking. Als k- even getal ( k = 2S), Dat
loggen A N 2S = 2S loggen A |N | (A > 0, A ≠ 1, N ≠ 0).
P5. Formule om naar een andere basis te verhuizen:
in het bijzonder als N = B, wij krijgen
(A > 0, A ≠ 1, B > 0, B ≠ 1). (2)Met behulp van de eigenschappen P4 en P5 is het eenvoudig te verkrijgen volgende eigenschappen
en, indien in (5) C- even getal ( C = 2N), plaatsvindt
Laten we de belangrijkste eigenschappen van de logaritmische functie opsommen F (X) = logboek A X :
1. Het definitiedomein van een logaritmische functie is de verzameling positieve getallen.
2. Het waardenbereik van de logaritmische functie is een set echte cijfers.
3. Wanneer A> 1 logaritmische functie is strikt stijgend (0< X 1 < X 2log A X 1 < logA X 2), en op 0< A < 1, - строго убывает (0 < X 1 < X 2log A X 1 > logboek A X 2).
4.loggen A 1 = 0 en loggen A A = 1 (A > 0, A ≠ 1).
5. Als A> 1, dan is de logaritmische functie negatief wanneer X(0;1) en positief op X(1;+∞), en als 0< A < 1, то логарифмическая функция положительна при X (0;1) en negatief bij X (1;+∞).
6. Als A> 1, dan is de logaritmische functie convex naar boven, en als A(0;1) - convex naar beneden.
De volgende uitspraken (zie bijvoorbeeld) worden gebruikt bij het oplossen van logaritmische vergelijkingen.
Denk je dat er nog tijd is vóór het Unified State Exam en dat je tijd hebt om je voor te bereiden? Misschien is dit zo. Maar hoe eerder een student met de voorbereiding begint, des te succesvoller hij de examens doorstaat. Vandaag hebben we besloten een artikel te wijden aan logaritmische ongelijkheden. Dit is een van de taken, wat een kans betekent om extra krediet te krijgen.
Weet jij al wat een logaritme is? Wij hopen het echt. Maar ook als je geen antwoord op deze vraag hebt, is dat geen probleem. Begrijpen wat een logaritme is, is heel eenvoudig.

Waarom 4? Je moet het getal 3 tot deze macht verheffen om 81 te krijgen. Als je het principe eenmaal begrijpt, kun je doorgaan met complexere berekeningen.
Een paar jaar geleden heb je ongelijkheid meegemaakt. En sindsdien kom je ze voortdurend tegen in de wiskunde. Als je problemen hebt met het oplossen van ongelijkheden, bekijk dan het betreffende gedeelte.
Nu we de concepten individueel hebben leren kennen, gaan we ze in het algemeen bekijken.
De eenvoudigste logaritmische ongelijkheid.

De eenvoudigste logaritmische ongelijkheden zijn niet beperkt tot dit voorbeeld; er zijn er nog drie, alleen met verschillende tekens. Waarom is dit nodig? Om beter te begrijpen hoe ongelijkheden met logaritmen kunnen worden opgelost. Laten we nu een toepasselijker voorbeeld geven, nog steeds vrij eenvoudig; we zullen complexe logaritmische ongelijkheden voor later bewaren.

Hoe dit op te lossen? Het begint allemaal bij ODZ. Als je ongelijkheid altijd gemakkelijk wilt oplossen, is het de moeite waard om er meer over te weten.
Wat is ODZ? ODZ voor logaritmische ongelijkheden
De afkorting staat voor het bereik van aanvaardbare waarden. Deze formulering komt vaak voor in taken voor het Unified State Exam. ODZ zal niet alleen nuttig voor u zijn in het geval van logaritmische ongelijkheden.
Kijk nog eens naar het bovenstaande voorbeeld. We zullen de ODZ op basis daarvan bekijken, zodat u het principe begrijpt en het oplossen van logaritmische ongelijkheden geen vragen oproept. Uit de definitie van een logaritme volgt dat 2x+4 groter moet zijn dan nul. In ons geval betekent dit het volgende.

Dit getal moet per definitie positief zijn. Los de hierboven gepresenteerde ongelijkheid op. Dit kan zelfs mondeling worden gedaan; hier is het duidelijk dat X niet kleiner kan zijn dan 2. De oplossing voor de ongelijkheid zal de definitie van het bereik van aanvaardbare waarden zijn.
Laten we nu verder gaan met het oplossen van de eenvoudigste logaritmische ongelijkheid.

We negeren de logaritmen zelf van beide kanten van de ongelijkheid. Wat houden we als resultaat over? Simpele ongelijkheid.

Het is niet moeilijk op te lossen. X moet groter zijn dan -0,5. Nu combineren we de twee verkregen waarden tot een systeem. Dus,

Dit zal het bereik zijn van acceptabele waarden voor de logaritmische ongelijkheid die wordt overwogen.
Waarom hebben we überhaupt ODZ nodig? Dit is een kans om onjuiste en onmogelijke antwoorden uit te sluiten. Als het antwoord niet binnen het bereik van aanvaardbare waarden ligt, heeft het antwoord eenvoudigweg geen zin. Dit is de moeite waard om lang te onthouden, omdat het bij het Unified State Exam vaak nodig is om naar ODZ te zoeken, en het gaat niet alleen om logaritmische ongelijkheden.
Algoritme voor het oplossen van logaritmische ongelijkheid
De oplossing bestaat uit verschillende fasen. Eerst moet u het bereik van acceptabele waarden vinden. Er zullen twee betekenissen zijn in de ODZ, dit hebben we hierboven besproken. Vervolgens moet je de ongelijkheid zelf oplossen. De oplossingsmethoden zijn als volgt:
- vermenigvuldiger vervangingsmethode;
- ontleding;
- rationalisatie methode.
Afhankelijk van de situatie is het de moeite waard om een van de bovenstaande methoden te gebruiken. Laten we direct naar de oplossing gaan. Laten we de meest populaire methode onthullen, die in bijna alle gevallen geschikt is voor het oplossen van Unified State Examination-taken. Vervolgens zullen we kijken naar de ontbindingsmethode. Het kan helpen als je een bijzonder lastige ongelijkheid tegenkomt. Een algoritme voor het oplossen van logaritmische ongelijkheid dus.
Voorbeelden van oplossingen :

Het is niet voor niets dat we precies deze ongelijkheid hebben genomen! Besteed aandacht aan de basis. Onthoud: als het groter is dan één, blijft het teken hetzelfde bij het vinden van het bereik van acceptabele waarden; anders moet u het ongelijkheidsteken wijzigen.
Als resultaat krijgen we de ongelijkheid:

Nu reduceren we de linkerkant tot de vorm van de vergelijking gelijk aan nul. In plaats van het ‘kleiner dan’-teken plaatsen we ‘is gelijk aan’ en lossen we de vergelijking op. Zo zullen we de ODZ vinden. We hopen dat u geen problemen zult ondervinden bij het oplossen van zo'n eenvoudige vergelijking. De antwoorden zijn -4 en -2. Dat is niet alles. U moet deze punten in de grafiek weergeven door “+” en “-” te plaatsen. Wat moet hiervoor gedaan worden? Vervang de getallen uit de intervallen door de uitdrukking. Waar de waarden positief zijn, plaatsen we daar “+”.
Antwoord: x kan niet groter zijn dan -4 en kleiner dan -2.
We hebben het bereik van acceptabele waarden alleen voor de linkerkant gevonden, nu moeten we het bereik van acceptabele waarden voor de rechterkant vinden. Dit is veel gemakkelijker. Antwoord: -2. We kruisen beide resulterende gebieden.
En pas nu beginnen we de ongelijkheid zelf aan te pakken.

Laten we het zo veel mogelijk vereenvoudigen om het gemakkelijker op te lossen.

We gebruiken opnieuw de intervalmethode in de oplossing. Laten we de berekeningen overslaan; alles is al duidelijk uit het vorige voorbeeld. Antwoord.

Maar deze methode is geschikt als de logaritmische ongelijkheid dezelfde grondtal heeft.
Logaritmische vergelijkingen en ongelijkheden oplossen met om verschillende redenen veronderstelt een initiële reductie tot één base. Gebruik vervolgens de hierboven beschreven methode. Maar er is meer moeilijk geval. Laten we een van de meest overwegen complexe soorten logaritmische ongelijkheden.
Logaritmische ongelijkheden met variabele basis
Hoe kunnen ongelijkheden met dergelijke kenmerken worden opgelost? Ja, en zulke mensen zijn te vinden in het Unified State Examination. Het op de volgende manier oplossen van ongelijkheden zal ook uw voordeel opleveren educatief proces. Laten we het probleem in detail bekijken. Laten we de theorie achterwege laten en direct naar de praktijk gaan. Om logaritmische ongelijkheden op te lossen, volstaat het om één keer vertrouwd te raken met het voorbeeld.

Om een logaritmische ongelijkheid van de gepresenteerde vorm op te lossen, is het noodzakelijk om de rechterkant terug te brengen tot een logaritme met hetzelfde grondtal. Het principe lijkt op gelijkwaardige overgangen. Als gevolg hiervan zal de ongelijkheid er zo uitzien.

Eigenlijk rest ons alleen nog het creëren van een systeem van ongelijkheden zonder logaritmen. Met behulp van de rationalisatiemethode gaan we verder naar een gelijkwaardig systeem van ongelijkheden. U zult de regel zelf begrijpen wanneer u de juiste waarden vervangt en hun wijzigingen volgt. Het systeem zal de volgende ongelijkheden hebben.

Wanneer u de rationalisatiemethode gebruikt bij het oplossen van ongelijkheden, moet u het volgende onthouden: één moet worden afgetrokken van de basis, x wordt, per definitie van de logaritme, afgetrokken van beide zijden van de ongelijkheid (rechts van links), twee uitdrukkingen worden vermenigvuldigd en ingesteld onder het oorspronkelijke teken ten opzichte van nul.
Verdere oplossing wordt uitgevoerd met behulp van de intervalmethode, alles is hier eenvoudig. Het is belangrijk dat u de verschillen in oplossingsmethoden begrijpt, dan zal alles gemakkelijk uitwerken.
Er zijn veel nuances in logaritmische ongelijkheden. De eenvoudigste zijn vrij eenvoudig op te lossen. Hoe kun je ze allemaal zonder problemen oplossen? Je hebt alle antwoorden in dit artikel al ontvangen. Nu heb je een lange oefening voor je. Oefen voortdurend met het oplossen van verschillende problemen tijdens het examen en je zult de hoogste score kunnen behalen. Veel succes bij uw moeilijke taak!
Van de hele verscheidenheid aan logaritmische ongelijkheden worden ongelijkheden met een variabele basis afzonderlijk bestudeerd. Ze worden opgelost met behulp van een speciale formule, die om de een of andere reden zelden op school wordt onderwezen:
log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0
In plaats van het selectievakje “∨” kunt u elk ongelijkheidsteken plaatsen: min of meer. Het belangrijkste is dat bij beide ongelijkheden de tekens hetzelfde zijn.
Op deze manier komen we af van logaritmen en reduceren we het probleem tot een rationele ongelijkheid. Dit laatste is veel gemakkelijker op te lossen, maar als je logaritmen weggooit, kunnen er extra wortels verschijnen. Om ze af te sluiten, volstaat het om het bereik van acceptabele waarden te vinden. Als u de ODZ van een logaritme bent vergeten, raad ik u ten zeerste aan deze te herhalen - zie "Wat is een logaritme".
Alles met betrekking tot het bereik van acceptabele waarden moet afzonderlijk worden opgeschreven en opgelost:
f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.
Deze vier ongelijkheden vormen een systeem en moeten tegelijkertijd worden vervuld. Wanneer het bereik van aanvaardbare waarden is gevonden, hoeft het alleen nog maar te worden doorkruist met de oplossing van de rationele ongelijkheid - en het antwoord is klaar.
Taak. Los de ongelijkheid op:
Laten we eerst de ODZ van de logaritme opschrijven:
Aan de eerste twee ongelijkheden wordt automatisch voldaan, maar aan de laatste moet worden uitgeschreven. Omdat het kwadraat van een getal nul is als en slechts als het getal zelf nul is, geldt:
x 2 + 1 ≠ 1;
x2 ≠ 0;
x ≠ 0.
Het blijkt dat de ODZ van de logaritme alle getallen is behalve nul: x ∈ (−∞ 0)∪(0; +∞). Nu lossen we de belangrijkste ongelijkheid op:

We maken de overgang van logaritmische ongelijkheid naar rationele ongelijkheid. De oorspronkelijke ongelijkheid heeft een ‘kleiner dan’-teken, wat betekent dat de resulterende ongelijkheid ook een ‘kleiner dan’-teken moet hebben. Wij hebben:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x) · (3 + x) · x 2< 0.
De nullen van deze uitdrukking zijn: x = 3; x = −3; x = 0. Bovendien is x = 0 een wortel van de tweede veelheid, wat betekent dat het teken van de functie niet verandert als je er doorheen gaat. Wij hebben:

We krijgen x ∈ (−∞ −3)∪(3; +∞). Deze set is volledig opgenomen in de ODZ van de logaritme, wat betekent dat dit het antwoord is.
Logaritmische ongelijkheden omzetten
Vaak is de oorspronkelijke ongelijkheid anders dan die hierboven. Dit kan eenvoudig worden gecorrigeerd met behulp van de standaardregels voor het werken met logaritmen - zie “Basiseigenschappen van logaritmen”. Namelijk:
- Elk getal kan worden weergegeven als een logaritme met een bepaald grondtal;
- De som en het verschil van logaritmen met dezelfde grondtallen kunnen worden vervangen door één logaritme.
Afzonderlijk zou ik u willen herinneren aan het bereik van aanvaardbare waarden. Omdat er meerdere logaritmen in de oorspronkelijke ongelijkheid kunnen voorkomen, is het nodig om de VA van elk ervan te vinden. Dus, algemeen schema oplossingen voor logaritmische ongelijkheden zijn als volgt:
- Zoek de VA van elke logaritme die in de ongelijkheid is opgenomen;
- Reduceer de ongelijkheid tot een standaardongelijkheid met behulp van de formules voor het optellen en aftrekken van logaritmen;
- Los de resulterende ongelijkheid op met behulp van het hierboven gegeven schema.
Taak. Los de ongelijkheid op:
Laten we het definitiedomein (DO) van de eerste logaritme vinden:
We lossen op met behulp van de intervalmethode. De nulpunten van de teller vinden:
3x − 2 = 0;
x = 2/3.
Dan - de nullen van de noemer:
x − 1 = 0;
x = 1.
We markeren nullen en tekens op de coördinatenpijl:

We krijgen x ∈ (−∞ 2/3)∪(1; +∞). De tweede logaritme heeft dezelfde VA. Als je me niet gelooft, kun je het controleren. Nu transformeren we de tweede logaritme zodat het grondtal twee is:
Zoals u kunt zien, zijn de drieën aan de basis en vóór de logaritme verkleind. We hebben twee logaritmes met hetzelfde grondtal. Laten we ze optellen:

logboek 2 (x − 1) 2< 2;
logboek 2 (x − 1) 2< log 2 2 2 .
We hebben de standaard logaritmische ongelijkheid verkregen. We ontdoen ons van logaritmen met behulp van de formule. Omdat de oorspronkelijke ongelijkheid een “kleiner dan”-teken bevat, is het resultaat rationele expressie moet ook kleiner zijn dan nul. Wij hebben:
(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2)(2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).
We hebben twee setjes:
- ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
- Kandidaatantwoord: x ∈ (−1; 3).
Het blijft nodig om deze sets te doorkruisen - we krijgen het echte antwoord:

We zijn geïnteresseerd in het snijpunt van verzamelingen, dus selecteren we intervallen die op beide pijlen gearceerd zijn. We krijgen x ∈ (−1; 2/3)∪(1; 3) - alle punten zijn lek.
Logaritmische ongelijkheden
In eerdere lessen maakten we kennis met logaritmische vergelijkingen en nu weten we wat ze zijn en hoe we ze kunnen oplossen. De les van vandaag zal gewijd zijn aan de studie van logaritmische ongelijkheden. Wat zijn deze ongelijkheden en wat is het verschil tussen het oplossen van een logaritmische vergelijking en een ongelijkheid?
Logaritmische ongelijkheden zijn ongelijkheden waarbij een variabele onder het logaritmeteken of aan de basis ervan verschijnt.
Of we kunnen ook zeggen dat een logaritmische ongelijkheid een ongelijkheid is waarvan de onbekende waarde, zoals in een logaritmische vergelijking, zal verschijnen onder het teken van de logaritme.
De eenvoudigste logaritmische ongelijkheden hebben de volgende vorm:
waarbij f(x) en g(x) enkele uitdrukkingen zijn die afhankelijk zijn van x.
Laten we dit eens bekijken met behulp van dit voorbeeld: f(x)=1+2x+x2, g(x)=3x−1.
Logaritmische ongelijkheden oplossen
Voordat we logaritmische ongelijkheden oplossen, is het de moeite waard om op te merken dat ze, wanneer opgelost, vergelijkbaar zijn met exponentiële ongelijkheden, namelijk:
Ten eerste moeten we, wanneer we van logaritmen naar uitdrukkingen onder het logaritmeteken gaan, ook de basis van de logaritme met één vergelijken;
Ten tweede moeten we, wanneer we een logaritmische ongelijkheid oplossen met behulp van een verandering van variabelen, ongelijkheden met betrekking tot de verandering oplossen totdat we de eenvoudigste ongelijkheid krijgen.
Maar jij en ik hebben soortgelijke aspecten van het oplossen van logaritmische ongelijkheden overwogen. Laten we nu eens kijken naar een nogal significant verschil. Jij en ik weten dat de logaritmische functie een beperkt definitiedomein heeft. Daarom moeten we bij het overstappen van logaritmen naar uitdrukkingen onder het logaritmeteken rekening houden met het bereik van toegestane waarden (ADV).
Dat wil zeggen dat er rekening mee moet worden gehouden dat u en ik bij het oplossen van een logaritmische vergelijking eerst de wortels van de vergelijking kunnen vinden en vervolgens deze oplossing kunnen controleren. Maar het oplossen van een logaritmische ongelijkheid zal op deze manier niet werken, omdat het bij het overstappen van logaritmen naar uitdrukkingen onder het logaritmeteken nodig zal zijn om de ODZ van de ongelijkheid op te schrijven.
Bovendien is het de moeite waard eraan te denken dat de theorie van ongelijkheid bestaat uit reële getallen, die positief zijn en negatieve getallen, evenals het getal 0.
Als het getal “a” bijvoorbeeld positief is, moet u de volgende notatie gebruiken: a >0. In dit geval zullen zowel de som als het product van deze getallen ook positief zijn.
Het belangrijkste principe voor het oplossen van een ongelijkheid is om deze te vervangen door een eenvoudigere ongelijkheid, maar het belangrijkste is dat deze gelijkwaardig is aan de gegeven ongelijkheid. Verder hebben we ook een ongelijkheid verkregen en deze opnieuw vervangen door een ongelijkheid met een eenvoudiger vorm, enz.
Bij het oplossen van ongelijkheden met een variabele moet je alle oplossingen vinden. Als twee ongelijkheden dezelfde variabele x hebben, dan zijn dergelijke ongelijkheden gelijkwaardig, op voorwaarde dat hun oplossingen samenvallen.
Bij het uitvoeren van taken voor het oplossen van logaritmische ongelijkheden moet u onthouden dat wanneer a > 1, de logaritmische functie toeneemt, en wanneer 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Methoden voor het oplossen van logaritmische ongelijkheden
Laten we nu eens kijken naar enkele van de methoden die worden gebruikt bij het oplossen van logaritmische ongelijkheden. Voor beter begrip en assimilatie, we zullen proberen ze te begrijpen aan de hand van specifieke voorbeelden.
We weten allemaal dat de eenvoudigste logaritmische ongelijkheid de volgende vorm heeft:
Bij deze ongelijkheid is V – een van de volgende ongelijkheidstekens:<,>, ≤ of ≥.
Wanneer de basis van een gegeven logaritme groter is dan één (a>1), waardoor de overgang wordt gemaakt van logaritmen naar uitdrukkingen onder het logaritmeteken, dan blijft in deze versie het ongelijkheidsteken behouden en zal de ongelijkheid de volgende vorm hebben:
wat gelijkwaardig is aan dit systeem:

In het geval dat de basis van de logaritme groter is dan nul en kleiner dan één (0 Dit is gelijk aan dit systeem: Laten we eens kijken naar meer voorbeelden van het oplossen van de eenvoudigste logaritmische ongelijkheden die in de onderstaande afbeelding worden weergegeven: Oefening. Laten we proberen deze ongelijkheid op te lossen: Het bereik van aanvaardbare waarden oplossen. Laten we nu proberen de rechterkant te vermenigvuldigen met: Laten we eens kijken wat we kunnen bedenken: Laten we nu verder gaan met het converteren van sublogaritmische uitdrukkingen. Vanwege het feit dat de basis van de logaritme 0 is< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; En hieruit volgt dat het interval dat we hebben verkregen volledig tot de ODZ behoort en een oplossing is voor een dergelijke ongelijkheid. Dit is het antwoord dat we kregen: Laten we nu proberen te analyseren wat we nodig hebben om logaritmische ongelijkheden met succes op te lossen? Concentreer eerst al uw aandacht en probeer geen fouten te maken bij het uitvoeren van de transformaties die in deze ongelijkheid worden gegeven. We moeten ook niet vergeten dat het bij het oplossen van dergelijke ongelijkheden noodzakelijk is om uitbreidingen en inkrimpingen van de ongelijkheden te vermijden, wat kan leiden tot het verlies of het verwerven van externe oplossingen. Ten tweede moet je bij het oplossen van logaritmische ongelijkheden logisch leren denken en het verschil begrijpen tussen concepten zoals een systeem van ongelijkheden en een reeks ongelijkheden, zodat je gemakkelijk oplossingen voor de ongelijkheid kunt selecteren, terwijl je je laat leiden door de DL ervan. Ten derde, om dergelijke ongelijkheden met succes op te lossen, moet ieder van jullie alle eigenschappen van elementaire functies perfect kennen en hun betekenis duidelijk begrijpen. Dergelijke functies omvatten niet alleen logaritmische, maar ook rationele, machts-, trigonometrische, enz., kortom al die functies die je tijdens de schoolalgebra hebt bestudeerd. Zoals u kunt zien, is er, nadat u het onderwerp logaritmische ongelijkheden heeft bestudeerd, niets moeilijks aan het oplossen van deze ongelijkheden, op voorwaarde dat u voorzichtig en volhardend bent in het bereiken van uw doelen. Om problemen bij het oplossen van ongelijkheden te voorkomen, moet je zoveel mogelijk oefenen, verschillende taken oplossen en tegelijkertijd de basismethoden onthouden voor het oplossen van dergelijke ongelijkheden en hun systemen. Als u er niet in slaagt logaritmische ongelijkheden op te lossen, moet u uw fouten zorgvuldig analyseren om er in de toekomst niet meer op terug te komen. Om het onderwerp beter te begrijpen en het behandelde materiaal te consolideren, lost u de volgende ongelijkheden op: Definitie van logaritme De eenvoudigste manier om het wiskundig te schrijven is: De definitie van logaritme kan op een andere manier worden geschreven: Let op de beperkingen die worden opgelegd aan de basis van de logaritme ( A) en naar de sublogaritmische uitdrukking ( X). In de toekomst zullen deze voorwaarden belangrijke beperkingen voor OD worden, waarmee rekening moet worden gehouden bij het oplossen van elke vergelijking met logaritmen. Dus nu moet er, naast de standaardvoorwaarden die leiden tot beperkingen op ODZ (positiviteit van uitdrukkingen onder de wortels van even machten, niet-gelijke noemer aan nul, enz.), ook rekening worden gehouden met de volgende voorwaarden: Merk op dat noch het grondtal van de logaritme, noch de sublogaritmische uitdrukking gelijk kan zijn aan nul. Houd er ook rekening mee dat de logaritmewaarde zelf alle mogelijke waarden kan aannemen, d.w.z. De logaritme kan positief, negatief of nul zijn. Logaritmen hebben veel verschillende eigenschappen die voortvloeien uit de eigenschappen van machten en de definitie van een logaritme. Laten we ze opsommen. Dus de eigenschappen van logaritmen: Logaritme van het product: Logaritme van een breuk: De graad uit het logaritmeteken halen: Let vooral goed op die van de laatst genoemde eigenschappen waarin het modulusteken verschijnt nadat de graad is behaald. Vergeet niet dat wanneer u een even macht buiten het logaritmeteken, onder de logaritme of aan de basis plaatst, u het modulusteken moet verlaten. Andere nuttige eigenschappen van logaritmen: De laatste eigenschap wordt heel vaak gebruikt in complexe logaritmische vergelijkingen en ongelijkheden. Hij moet net zo goed herinnerd worden als iedereen, ook al wordt hij vaak vergeten. De eenvoudigste logaritmische vergelijkingen zien er als volgt uit: En hun oplossing wordt gegeven door een formule die direct volgt uit de definitie van de logaritme: Andere eenvoudigste logaritmische vergelijkingen zijn die welke, met behulp van algebraïsche transformaties en de bovenstaande formules en eigenschappen van logaritmen, kunnen worden teruggebracht tot de vorm: De oplossing voor dergelijke vergelijkingen, rekening houdend met de ODZ, is als volgt: Enkele anderen logaritmische vergelijkingen met een variabele aan de basis kan worden teruggebracht tot de vorm: In dergelijke logaritmische vergelijkingen volgt de algemene vorm van de oplossing ook rechtstreeks uit de definitie van de logaritme. Alleen in dit geval zijn er aanvullende beperkingen voor DZ waarmee rekening moet worden gehouden. Als gevolg hiervan moet u, om een logaritmische vergelijking met een variabele in de basis op te lossen, het volgende systeem oplossen: Bij het oplossen van complexere logaritmische vergelijkingen die niet kunnen worden gereduceerd tot een van de hierboven gepresenteerde vergelijkingen, wordt deze ook actief gebruikt variabele vervangingsmethode. Zoals gewoonlijk moet u bij het gebruik van deze methode onthouden dat na het introduceren van de vervanging de vergelijking eenvoudiger moet worden en niet langer het oude onbekende moet bevatten. U moet er ook aan denken om omgekeerde vervanging van variabelen uit te voeren. Soms moet je bij het oplossen van logaritmische vergelijkingen ook gebruiken grafische methode. Deze methode bestaat uit het construeren van grafieken van functies die zich aan de linker- en rechterkant van de vergelijking bevinden, zo nauwkeurig mogelijk op één coördinatenvlak, en vervolgens het vinden van de coördinaten van hun snijpunten uit de tekening. De op deze manier verkregen wortels moeten worden gecontroleerd door vervanging in de oorspronkelijke vergelijking. Bij het oplossen van logaritmische vergelijkingen is het vaak ook nuttig groeperingsmethode. Bij het gebruik van deze methode is het belangrijkste om te onthouden dat: om het product van verschillende factoren gelijk te laten zijn aan nul, het noodzakelijk is dat ten minste één ervan gelijk is aan nul, en de rest bestond. Wanneer de factoren logaritmen of haakjes met logaritmen zijn, en niet alleen maar haakjes met variabelen zoals in rationale vergelijkingen, kunnen er veel fouten optreden. Omdat logaritmen veel beperkingen hebben in de regio waar ze voorkomen. Bij het beslissen systemen van logaritmische vergelijkingen meestal moet u de substitutiemethode of de variabele vervangingsmethode gebruiken. Als deze mogelijkheid bestaat, moet men er bij het oplossen van systemen van logaritmische vergelijkingen naar streven om ervoor te zorgen dat elk van de vergelijkingen van het systeem individueel in een vorm wordt gebracht waarin het mogelijk zal zijn om de overgang te maken van een logaritmische vergelijking naar een rationele. De eenvoudigste logaritmische ongelijkheden worden op ongeveer dezelfde manier opgelost als vergelijkbare vergelijkingen. Ten eerste moeten we, met behulp van algebraïsche transformaties en de eigenschappen van logaritmen, proberen ze in een vorm te brengen waarin de logaritmen aan de linker- en rechterkant van de ongelijkheid dezelfde bases zullen hebben, d.w.z. krijg een ongelijkheid van de vorm: Waarna je naar een rationele ongelijkheid moet gaan, rekening houdend met het feit dat deze overgang als volgt moet worden uitgevoerd: als de basis van de logaritme groter is dan één, hoeft het teken van de ongelijkheid niet te worden veranderd, en als de de basis van de logaritme kleiner is dan één, dan moet je het teken van de ongelijkheid in het tegenovergestelde veranderen (dit betekent dat je "minder" in "meer" verandert of omgekeerd). In dit geval is het niet nodig om de mintekens in plustekens te veranderen, waarbij de eerder geleerde regels worden omzeild. Laten we wiskundig opschrijven wat we krijgen als resultaat van het uitvoeren van een dergelijke transitie. Als de basis groter is dan één krijgen we: Als het grondtal van de logaritme kleiner is dan één, veranderen we het teken van ongelijkheid en krijgen we het volgende systeem: Zoals we zien, wordt bij het oplossen van logaritmische ongelijkheden, zoals gebruikelijk, ook rekening gehouden met de ODZ (dit is de derde voorwaarde in de bovenstaande systemen). Bovendien is het in dit geval mogelijk om niet de positiviteit van beide sublogaritmische uitdrukkingen te eisen, maar alleen de positiviteit van de kleinste ervan. Bij het beslissen logaritmische ongelijkheden met een variabele aan de basis logaritme, is het noodzakelijk om beide opties onafhankelijk te overwegen (wanneer de basis kleiner is dan één en groter dan één) en de oplossingen van deze gevallen in een set te combineren. Tegelijkertijd mogen we DL niet vergeten, d.w.z. over het feit dat zowel de basis als alle sublogaritmische uitdrukkingen positief moeten zijn. Dus bij het oplossen van een ongelijkheid van de vorm: We verkrijgen de volgende reeks systemen: Complexere logaritmische ongelijkheden kunnen ook worden opgelost door variabelen te veranderen. Sommige andere logaritmische ongelijkheden (zoals logaritmische vergelijkingen) vereisen de procedure waarbij de logaritme van beide zijden van de ongelijkheid of vergelijking naar dezelfde basis wordt gebracht om op te lossen. Er is dus sprake van subtiliteit bij het uitvoeren van een dergelijke procedure met logaritmische ongelijkheden. Houd er rekening mee dat wanneer logaritmen naar een grondtal groter dan één worden gebracht, het ongelijkheidsteken niet verandert, maar als het grondtal kleiner is dan één, wordt het ongelijkheidsteken omgekeerd. Als een logaritmische ongelijkheid niet kan worden gereduceerd tot een rationele ongelijkheid of kan worden opgelost door middel van substitutie, dan moet men in dit geval gebruik maken van gegeneraliseerde intervalmethode, die als volgt luidt: Om je succesvol voor te bereiden op de CT in onder meer natuurkunde en wiskunde, is het noodzakelijk om aan drie belangrijkste voorwaarden te voldoen: Succesvolle, ijverige en verantwoorde implementatie van deze drie punten stelt u in staat een uitstekend resultaat te laten zien op de CT, het maximale van wat u kunt. Als u denkt dat u een fout heeft gevonden in educatieve materialen, schrijf er dan per e-mail over. U kunt een bug ook melden aan sociaal netwerk(). Vermeld in de brief het onderwerp (natuurkunde of wiskunde), de naam of het nummer van het onderwerp of de toets, het nummer van het probleem of de plaats in de tekst (pagina) waar naar jouw mening een fout staat. Beschrijf ook wat de vermoedelijke fout is. Uw brief zal niet onopgemerkt blijven, de fout wordt verbeterd of u krijgt uitleg waarom het geen fout is.

Voorbeelden oplossen
![]()



3x > 24;
x > 8. ![]()
Wat is er nodig om logaritmische ongelijkheden op te lossen?
Huiswerk




![]()
![]()

![]()


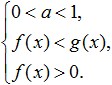

Hoe kun je je succesvol voorbereiden op de CT in natuurkunde en wiskunde?
Een fout gevonden?





