Įvadas
Logaritmai buvo išrasti siekiant pagreitinti ir supaprastinti skaičiavimus. Logaritmo idėja, tai yra, idėja išreikšti skaičius kaip tos pačios bazės galias, priklauso Michailui Stiefeliui. Tačiau Stiefelio laikais matematika nebuvo taip išvystyta ir logaritmo idėja nebuvo išvystyta. Vėliau logaritmus vienu metu ir nepriklausomai vienas nuo kito išrado škotų mokslininkas Johnas Napier (1550–1617), o šveicaras Jobstas Burgi (1552–1632) pirmasis paskelbė 1614 m. pavadinimu „Nuostabiosios logaritmų lentelės aprašymas“, Napier logaritmų teorija buvo pateikta pakankamai išsamiai. pilnai, logaritmų skaičiavimo metodas pateiktas paprasčiausias, todėl Napier nuopelnai logaritmų išradime yra didesni nei Bürgi. Bürgi dirbo prie stalų tuo pačiu metu kaip Napier, bet ilgą laiką laikė juos paslaptyje ir paskelbė tik 1620 m. Napier įsisavino logaritmo idėją apie 1594 m. nors lentelės buvo paskelbtos po 20 metų. Iš pradžių jis pavadino savo logaritmus „dirbtiniais skaičiais“, o tik tada pasiūlė šiuos „dirbtinius skaičius“ pavadinti vienu žodžiu „logaritmas“, kuris išvertus iš graikų kalbos reiškia „koreliuoti skaičiai“, vienas paimtas iš aritmetinės progresijos, o kitas iš specialiai jai parinkta geometrinė progresija. Pirmosios lentelės rusų kalba buvo išleistos 1703 m. dalyvaujant nuostabiam mokytojui XVIII a. L. F. Magnitskis. Kuriant logaritmų teoriją puiki vertė turėjo Peterburgo akademiko Leonhardo Eulerio darbų. Jis pirmasis logaritmus laikė atvirkštine laipsnio didinimo dalimi. Jis įvedė terminus „logaritmo bazė“ ir „mantisa“. paprastesni nei Napier logaritmai . Todėl dešimtainiai logaritmai kartais vadinami Briggso logaritmais. Terminą „charakteristika“ įvedė Briggsas.
Tais tolimais laikais, kai išminčiai pirmą kartą pradėjo galvoti apie lygybes, kuriose yra nežinomi kiekiai, tikriausiai nebuvo monetų ar piniginių. Tačiau buvo krūvos, taip pat puodai ir krepšeliai, kurie puikiai tiko kaip saugyklos, kuriose galėjo tilpti nežinomas kiekis daiktų. Senovės Mesopotamijos, Indijos, Kinijos, Graikijos matematinėse problemose nežinomi kiekiai išreiškė povų skaičių sode, bulių skaičių bandoje ir dalykų, į kuriuos buvo atsižvelgta dalijant turtą, visumą. Su tokiomis užduotimis gana sėkmingai susidorojo raštininkai, valdininkai ir kunigai, inicijuoti į slaptas žinias, gerai apmokyti sąskaitų mokslo.
Mus pasiekę šaltiniai rodo, kad senovės mokslininkai turėjo keletą bendrų metodų, kaip spręsti problemas su nežinomais kiekiais. Tačiau ne vienoje papiruso ar molio lentelėje nėra šių metodų aprašymo. Autoriai tik retkarčiais pateikdavo savo skaitinius skaičiavimus su šykščiais komentarais, tokiais kaip: „Žiūrėk!“, „Padaryk tai!“, „Radai tinkamą“. Šia prasme išimtis yra graikų matematiko Diofanto Aleksandriečio (III a.) „Aritmetika“ - lygčių sudarymo uždavinių rinkinys su sistemingu jų sprendimų pateikimu.
Tačiau pirmasis plačiai žinomas problemų sprendimo vadovas buvo IX amžiaus Bagdado mokslininko darbas. Muhamedas bin Musa al Khwarizmi. Žodis „al-jabr“ iš arabiško šio traktato pavadinimo – „Kitab al-jaber wal-mukabala“ („Atkūrimo ir opozicijos knyga“) laikui bėgant virto gerai žinomu žodžiu „algebra“, o kūrinys. pats al-Khwarizmi buvo pradinis taškas plėtojant lygčių sprendimo mokslą.
Logaritminės lygtys ir nelygybės
1. Logaritminės lygtys
Lygtis, kurioje yra nežinomasis po logaritmo ženklu arba jo pagrindu, vadinama logaritmine lygtimi.
Paprasčiausia logaritminė lygtis yra formos lygtis
žurnalas a x = b . (1)
Teiginys 1. Jeigu a > 0, a≠ 1, (1) lygtis bet kuriai realiai b turi unikalų sprendimą x = a b .
1 pavyzdys. Išspręskite lygtis:
a) žurnalas 2 x= 3, b) log 3 x= -1, c)
Sprendimas. Naudodami 1 teiginį gauname a) x= 2 3 arba x= 8; b) x= 3 -1 arba x= 1/3; c)
arba x = 1.Pateiksime pagrindines logaritmo savybes.
P1. Pagrindinė logaritminė tapatybė:
Kur a > 0, a≠ 1 ir b > 0.
P2. Teigiamų veiksnių sandaugos logaritmas lygi sumaišių faktorių logaritmai:
žurnalas a N 1 · N 2 = rąstas a N 1 + rąstas a N 2 (a > 0, a ≠ 1, N 1 > 0, N 2 > 0).
komentuoti. Jeigu N 1 · N 2 > 0, tada ypatybė P2 įgauna formą
žurnalas a N 1 · N 2 = rąstas a |N 1 | + žurnalas a |N 2 | (a > 0, a ≠ 1, N 1 · N 2 > 0).
P3. Dviejų teigiamų skaičių dalinio logaritmas yra lygus dividendo ir daliklio logaritmų skirtumui
komentuoti. Jeigu
, (kuris yra lygiavertis N 1 N 2 > 0), tada ypatybė P3 įgauna formąP4. Teigiamo skaičiaus galios logaritmas yra lygus eksponento sandaugai ir šio skaičiaus logaritmui:
žurnalas a N k = kžurnalas a N (a > 0, a ≠ 1, N > 0).
komentuoti. Jeigu k- lyginis skaičius ( k = 2s), tai
žurnalas a N 2s = 2sžurnalas a |N | (a > 0, a ≠ 1, N ≠ 0).
P5. Persikėlimo į kitą bazę formulė:
ypač jei N = b, gauname
(a > 0, a ≠ 1, b > 0, b ≠ 1). (2)Naudojant P4 ir P5 savybes, jį lengva gauti šias savybes
ir, jei nurodyta (5) c- lyginis skaičius ( c = 2n), laikosi
Išvardinkime pagrindines logaritminės funkcijos savybes f (x) = žurnalas a x :
1. Logaritminės funkcijos apibrėžimo sritis yra teigiamų skaičių aibė.
2. Logaritminės funkcijos reikšmių diapazonas - rinkinys realūs skaičiai.
3. Kada a> 1 logaritminė funkcija griežtai didėja (0< x 1 < x 2log a x 1 < loga x 2) ir 0< a < 1, - строго убывает (0 < x 1 < x 2log a x 1 > žurnalas a x 2).
4.log a 1 = 0 ir log a a = 1 (a > 0, a ≠ 1).
5. Jeigu a> 1, tada logaritminė funkcija yra neigiama, kai x(0;1) ir teigiamas ties x(1;+∞), o jei 0< a < 1, то логарифмическая функция положительна при x (0;1) ir neigiamas at x (1;+∞).
6. Jeigu a> 1, tada logaritminė funkcija yra išgaubta į viršų, o jei a(0;1) – išgaubta žemyn.
Sprendžiant logaritmines lygtis naudojami šie teiginiai (žr., pvz.).
Ar manote, kad iki vieningo valstybinio egzamino dar liko laiko ir turėsite laiko pasiruošti? Galbūt taip ir yra. Bet bet kuriuo atveju, kuo anksčiau studentas pradeda ruoštis, tuo sėkmingiau jis išlaiko egzaminus. Šiandien nusprendėme skirti straipsnį logaritminėms nelygybėms. Tai viena iš užduočių, reiškiančių galimybę gauti papildomą kreditą.
Ar jau žinai, kas yra logaritmas? Labai tikimės. Bet net jei neturite atsakymo į šį klausimą, tai nėra problema. Suprasti, kas yra logaritmas, labai paprasta.

Kodėl 4? Turite padidinti skaičių 3 iki šios galios, kad gautumėte 81. Kai suprasite principą, galite pereiti prie sudėtingesnių skaičiavimų.
Prieš kelerius metus išgyvenote nelygybę. Ir nuo to laiko jūs nuolat susiduriate su jais matematikoje. Jei kyla problemų sprendžiant nelygybes, peržiūrėkite atitinkamą skyrių.
Dabar, kai susipažinome su sąvokomis atskirai, pereikime prie jų bendro nagrinėjimo.
Paprasčiausia logaritminė nelygybė.

Paprasčiausios logaritminės nelygybės neapsiriboja šiuo pavyzdžiu, yra dar trys, tik su skirtingais ženklais. Kodėl tai būtina? Norėdami geriau suprasti, kaip logaritmais išspręsti nelygybes. Dabar pateikime tinkamesnį pavyzdį, vis dar gana paprastą, sudėtingas logaritmines nelygybes paliksime vėlesniam laikui.

Kaip tai išspręsti? Viskas prasideda nuo ODZ. Verta apie tai sužinoti daugiau, jei norite visada lengvai išspręsti bet kokią nelygybę.
Kas yra ODZ? ODZ logaritminėms nelygybėms
Santrumpa reiškia priimtinų verčių diapazoną. Ši formuluotė dažnai atsiranda atliekant vieningo valstybinio egzamino užduotis. ODZ jums bus naudingas ne tik logaritminių nelygybių atveju.
Dar kartą pažiūrėkite į aukščiau pateiktą pavyzdį. Remdamiesi juo svarstysime ODZ, kad suprastumėte principą, o logaritminių nelygybių sprendimas nekeltų klausimų. Iš logaritmo apibrėžimo išplaukia, kad 2x+4 turi būti didesnis už nulį. Mūsų atveju tai reiškia štai ką.

Šis skaičius pagal apibrėžimą turi būti teigiamas. Išspręskite aukščiau pateiktą nelygybę. Tai galima padaryti net žodžiu, čia aišku, kad X negali būti mažesnis nei 2. Nelygybės sprendimas bus priimtinų reikšmių diapazono apibrėžimas.
Dabar pereikime prie paprasčiausios logaritminės nelygybės sprendimo.

Mes atmetame pačius logaritmus iš abiejų nelygybės pusių. Kas mums liko dėl to? Paprasta nelygybė.

Tai nesunku išspręsti. X turi būti didesnis nei -0,5. Dabar mes sujungiame dvi gautas reikšmes į sistemą. Taigi,

Tai bus nagrinėjamos logaritminės nelygybės priimtinų verčių diapazonas.
Kodėl mums apskritai reikia ODZ? Tai galimybė atsikratyti neteisingų ir neįmanomų atsakymų. Jei atsakymas nepatenka į priimtinų verčių diapazoną, atsakymas tiesiog neturi prasmės. Tai verta prisiminti ilgą laiką, nes vieningame valstybiniame egzamine dažnai reikia ieškoti ODZ, ir tai susiję ne tik su logaritminėmis nelygybėmis.
Logaritminės nelygybės sprendimo algoritmas
Sprendimas susideda iš kelių etapų. Pirmiausia turite rasti priimtinų verčių diapazoną. ODZ bus dvi reikšmės, mes tai aptarėme aukščiau. Toliau turime išspręsti pačią nelygybę. Sprendimo metodai yra tokie:
- daugiklio pakeitimo metodas;
- skilimas;
- racionalizavimo metodas.
Atsižvelgiant į situaciją, verta naudoti vieną iš aukščiau pateiktų metodų. Pereikime tiesiai prie sprendimo. Atskleisime populiariausią metodą, kuris tinka spręsti vieningo valstybinio egzamino užduotis beveik visais atvejais. Toliau apžvelgsime skaidymo metodą. Tai gali padėti, jei susidursite su ypač sudėtinga nelygybe. Taigi, logaritminės nelygybės sprendimo algoritmas.
Sprendimų pavyzdžiai :

Ne veltui mes paėmėme būtent šią nelygybę! Atkreipkite dėmesį į pagrindą. Atsiminkite: jei jis didesnis už vienetą, randant priimtinų reikšmių diapazoną, ženklas išlieka toks pat; kitu atveju reikia pakeisti nelygybės ženklą.
Dėl to gauname nelygybę:

Dabar kairę pusę sumažiname iki lygties formos, lygios nuliui. Vietoj ženklo „mažiau nei“ dedame „lygu“ ir išsprendžiame lygtį. Taigi, mes rasime ODZ. Tikimės, kad jums nekils problemų sprendžiant tokią paprastą lygtį. Atsakymai yra -4 ir -2. Tai dar ne viskas. Turite parodyti šiuos taškus grafike, padėdami „+“ ir „-“. Ką reikia padaryti dėl to? Pakeiskite skaičius iš intervalų į išraišką. Kai reikšmės yra teigiamos, ten įdedame „+“.
Atsakymas: x negali būti didesnis nei -4 ir mažesnis nei -2.
Mes radome priimtinų verčių diapazoną tik kairiajai pusei, dabar turime rasti priimtinų verčių diapazoną dešinėje pusėje. Tai daug lengviau. Atsakymas: -2. Mes susikertame abi gautas sritis.
Ir tik dabar pradedame spręsti pačią nelygybę.

Kiek įmanoma supaprastinkime, kad būtų lengviau išspręsti.

Sprendime vėl naudojame intervalo metodą. Praleiskime skaičiavimus, viskas jau aišku iš ankstesnio pavyzdžio. Atsakymas.

Bet šis metodas tinka, jei logaritminė nelygybė turi tuos pačius pagrindus.
Spręsdami logaritmines lygtis ir nelygybes su dėl skirtingų priežasčių suponuoja pradinį sumažinimą iki vienos bazės. Tada naudokite aukščiau aprašytą metodą. Bet yra ir daugiau sunkus atvejis. Panagrinėkime vieną iš labiausiai sudėtingos rūšys logaritmines nelygybes.
Logaritminės nelygybės su kintamu pagrindu
Kaip išspręsti tokias charakteristikas turinčias nelygybes? Taip, ir tokių žmonių galima rasti Vieningame valstybiniame egzamine. Nelygybių sprendimas tokiu būdu taip pat bus naudingas jums ugdymo procesas. Pažvelkime į problemą išsamiai. Išmeskime teoriją ir eikime tiesiai į praktiką. Norint išspręsti logaritmines nelygybes, pakanka vieną kartą susipažinti su pavyzdžiu.

Norint išspręsti pateiktos formos logaritminę nelygybę, reikia sumažinti dešinę pusę iki logaritmo su ta pačia baze. Principas primena lygiaverčius perėjimus. Dėl to nelygybė atrodys taip.

Tiesą sakant, belieka sukurti nelygybių sistemą be logaritmų. Naudodami racionalizacijos metodą pereiname prie lygiavertės nelygybių sistemos. Pačią taisyklę suprasite, kai pakeisite atitinkamas reikšmes ir stebėsite jų pokyčius. Sistema turės tokias nelygybes.

Sprendžiant nelygybes naudojant racionalizacijos metodą, reikia atsiminti: vieną reikia atimti iš pagrindo, x pagal logaritmo apibrėžimą atimama iš abiejų nelygybės pusių (dešinė iš kairės), dvi išraiškos padauginamos ir nustatyti po pirminiu ženklu nulio atžvilgiu.
Tolesnis sprendimas atliekamas naudojant intervalų metodą, čia viskas paprasta. Jums svarbu suprasti sprendimo būdų skirtumus, tada viskas pradės lengvai klotis.
Logaritminėse nelygybėse yra daug niuansų. Paprasčiausius iš jų gana lengva išspręsti. Kaip galite išspręsti kiekvieną iš jų be problemų? Šiame straipsnyje jau gavote visus atsakymus. Dabar jūsų laukia ilga praktika. Nuolat treniruokitės spręsdami įvairias egzamine problemas ir galėsite gauti aukščiausią balą. Sėkmės jums atliekant sunkią užduotį!
Iš visos logaritminių nelygybių įvairovės atskirai nagrinėjamos nelygybės su kintamu pagrindu. Jie sprendžiami naudojant specialią formulę, kuri dėl kokių nors priežasčių retai mokoma mokykloje:
log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0
Vietoj žymės langelio „∨“ galite įdėti bet kokį nelygybės ženklą: daugiau ar mažiau. Svarbiausia, kad abiejose nelygybėse ženklai būtų vienodi.
Taip atsikratome logaritmų ir sumažiname problemą iki racionalios nelygybės. Pastarąjį išspręsti daug lengviau, tačiau atmetus logaritmus gali atsirasti papildomų šaknų. Norint juos nupjauti, pakanka rasti priimtinų verčių diapazoną. Jei pamiršote logaritmo ODZ, primygtinai rekomenduoju jį pakartoti – žr. „Kas yra logaritmas“.
Viskas, kas susiję su priimtinų verčių diapazonu, turi būti užrašoma ir išspręsta atskirai:
f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.
Šios keturios nelygybės sudaro sistemą ir turi būti tenkinamos vienu metu. Kai randamas priimtinų reikšmių diapazonas, belieka jį susikirsti su racionalios nelygybės sprendimu – ir atsakymas paruoštas.
Užduotis. Išspręskite nelygybę:
Pirmiausia užrašykite logaritmo ODZ:
Pirmosios dvi nelygybės tenkinamos automatiškai, tačiau paskutinė turės būti išrašyta. Kadangi skaičiaus kvadratas yra nulis tada ir tik tada, kai pats skaičius yra nulis, turime:
x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.
Pasirodo, kad logaritmo ODZ yra visi skaičiai, išskyrus nulį: x ∈ (−∞ 0)∪(0; +∞). Dabar išsprendžiame pagrindinę nelygybę:

Mes pereiname nuo logaritminės nelygybės prie racionalios. Pradinė nelygybė turi ženklą „mažiau nei“, o tai reiškia, kad gauta nelygybė taip pat turi turėti „mažiau nei“ ženklą. Turime:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 – x 2) x 2< 0;
(3 − x ) (3 + x ) x 2< 0.
Šios išraiškos nuliai yra: x = 3; x = –3; x = 0. Be to, x = 0 yra antrojo dauginio šaknis, vadinasi, einant pro ją funkcijos ženklas nekinta. Turime:

Gauname x ∈ (−∞ −3)∪(3; +∞). Šis rinkinys yra visiškai įtrauktas į logaritmo ODZ, o tai reiškia, kad tai yra atsakymas.
Logaritminių nelygybių konvertavimas
Dažnai pradinė nelygybė skiriasi nuo aukščiau pateiktos. Tai galima lengvai ištaisyti naudojant standartines darbo su logaritmais taisykles – žr. „Pagrindinės logaritmų savybės“. Būtent:
- Bet kuris skaičius gali būti pavaizduotas kaip logaritmas su duota baze;
- Logaritmų su vienodais pagrindais sumą ir skirtumą galima pakeisti vienu logaritmu.
Atskirai norėčiau priminti apie priimtinų verčių diapazoną. Kadangi pradinėje nelygybėje gali būti keli logaritmai, reikia rasti kiekvieno iš jų VA. Taigi, bendra schema logaritminių nelygybių sprendimai yra tokie:
- Raskite kiekvieno logaritmo, įtraukto į nelygybę, VA;
- Sumažinkite nelygybę iki standartinės, naudodami logaritmų pridėjimo ir atėmimo formules;
- Išspręskite gautą nelygybę pagal aukščiau pateiktą schemą.
Užduotis. Išspręskite nelygybę:
Raskime pirmojo logaritmo apibrėžimo sritį (DO):
Sprendžiame intervalo metodu. Skaitiklio nulių radimas:
3x − 2 = 0;
x = 2/3.
Tada - vardiklio nuliai:
x − 1 = 0;
x = 1.
Ant koordinačių rodyklės pažymime nulius ir ženklus:

Gauname x ∈ (−∞ 2/3)∪(1; +∞). Antrasis logaritmas turės tą patį VA. Jei netikite manimi, galite tai patikrinti. Dabar paverčiame antrąjį logaritmą taip, kad bazė būtų dvi:
Kaip matote, trys prie pagrindo ir prieš logaritmą buvo sumažinti. Gavome du logaritmus su ta pačia baze. Sudėkime juos:

log 2 (x − 1) 2< 2;
log 2 (x − 1) 2< log 2 2 2 .
Gavome standartinę logaritminę nelygybę. Atsikratome logaritmų naudodami formulę. Kadangi pradinėje nelygybėje yra ženklas „mažiau nei“, gaunama racionali išraiška taip pat turi būti mažesnis už nulį. Turime:
(f (x) – g (x)) (k (x) – 1)< 0;
((x - 1) 2 - 2 2) (2 - 1)< 0;
x 2 - 2x + 1 - 4< 0;
x 2 - 2x - 3< 0;
(x – 3) (x + 1)< 0;
x ∈ (-1; 3).
Gavome du komplektus:
- ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
- Kandidatas į atsakymą: x ∈ (−1; 3).
Belieka susikirsti šias aibes - mes gauname tikrą atsakymą:

Mus domina aibių sankirta, todėl pasirenkame intervalus, kurie yra užtamsinti ant abiejų rodyklių. Gauname x ∈ (−1; 2/3)∪(1; 3) – visi taškai pradurti.
Logaritminės nelygybės
Ankstesnėse pamokose susipažinome su logaritminėmis lygtimis ir dabar žinome, kas jos yra ir kaip jas išspręsti. Šios dienos pamoka bus skirta logaritminių nelygybių tyrimui. Kas yra šios nelygybės ir kuo skiriasi logaritminės lygties sprendimas nuo nelygybės?
Logaritminės nelygybės yra nelygybės, kurių kintamasis yra po logaritmo ženklu arba jo pagrindu.
Arba taip pat galime pasakyti, kad logaritminė nelygybė yra nelygybė, kurioje jos nežinoma reikšmė, kaip ir logaritminėje lygtyje, atsiras po logaritmo ženklu.
Paprasčiausios logaritminės nelygybės turi tokią formą:
kur f(x) ir g(x) yra kai kurios išraiškos, kurios priklauso nuo x.
Pažvelkime į tai naudodami šį pavyzdį: f(x)=1+2x+x2, g(x)=3x−1.
Logaritminių nelygybių sprendimas
Prieš sprendžiant logaritmines nelygybes, verta paminėti, kad išspręstos jos yra panašios į eksponentinės nelygybės, būtent:
Pirma, pereinant nuo logaritmų prie išraiškų po logaritmo ženklu, taip pat turime palyginti logaritmo bazę su vienu;
Antra, sprendžiant logaritminę nelygybę naudojant kintamųjų pokytį, turime spręsti nelygybes pokyčio atžvilgiu, kol gausime paprasčiausią nelygybę.
Bet jūs ir aš svarstėme panašius logaritminių nelygybių sprendimo aspektus. Dabar atkreipkime dėmesį į gana reikšmingą skirtumą. Jūs ir aš žinome, kad logaritminė funkcija turi ribotą apibrėžimo sritį, todėl pereinant nuo logaritmų prie išraiškų po logaritmo ženklu, turime atsižvelgti į leistinų verčių diapazoną (ADV).
Tai reiškia, kad reikia atsižvelgti į tai, kad spręsdami logaritminę lygtį, jūs ir aš pirmiausia galime rasti lygties šaknis, o tada patikrinti šį sprendimą. Tačiau logaritminės nelygybės sprendimas taip neveiks, nes pereinant nuo logaritmų prie išraiškų po logaritmo ženklu, reikės užrašyti nelygybės ODZ.
Be to, verta prisiminti, kad nelygybių teorija susideda iš realiųjų skaičių, kurie yra teigiami ir neigiami skaičiai, taip pat skaičius 0.
Pavyzdžiui, kai skaičius „a“ yra teigiamas, reikia naudoti tokį žymėjimą: a >0. Šiuo atveju ir šių skaičių suma, ir sandauga taip pat bus teigiami.
Pagrindinis nelygybės sprendimo principas yra pakeisti ją paprastesne nelygybe, tačiau svarbiausia, kad ji būtų lygiavertė duotajai. Be to, mes taip pat gavome nelygybę ir vėl ją pakeitėme paprastesne forma ir pan.
Sprendžiant nelygybes su kintamuoju, reikia rasti visus jo sprendimus. Jei dvi nelygybės turi tą patį kintamąjį x, tai tokios nelygybės yra lygiavertės, jei jų sprendiniai sutampa.
Atlikdami logaritminių nelygybių sprendimo užduotis, turite atsiminti, kad kai a > 1, tada logaritminė funkcija didėja, o kai 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Logaritminių nelygybių sprendimo metodai
Dabar pažvelkime į kai kuriuos metodus, taikomus sprendžiant logaritmines nelygybes. Už geresnis supratimas ir asimiliaciją, bandysime juos suprasti pasitelkdami konkrečius pavyzdžius.
Visi žinome, kad paprasčiausia logaritminė nelygybė turi tokią formą:
Šioje nelygybėje V – yra vienas iš šių nelygybės ženklų:<,>, ≤ arba ≥.
Kai duoto logaritmo bazė yra didesnė už vieną (a>1), pereinant nuo logaritmų prie išraiškų po logaritmo ženklu, tada šioje versijoje nelygybės ženklas išsaugomas, o nelygybė bus tokia:
kuri yra lygiavertė šiai sistemai:

Tuo atveju, kai logaritmo bazė yra didesnė už nulį ir mažesnė už vieną (0 Tai atitinka šią sistemą: Pažvelkime į daugiau paprasčiausių logaritminių nelygybių sprendimo pavyzdžių, parodytų paveikslėlyje žemiau: Pratimai. Pabandykime išspręsti šią nelygybę: Priimtinų verčių diapazono sprendimas. Dabar pabandykime padauginti jo dešinę pusę iš: Pažiūrėkime, ką galime sugalvoti: Dabar pereikime prie sublogaritminių išraiškų konvertavimo. Dėl to, kad logaritmo pagrindas yra 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; Iš to išplaukia, kad gautas intervalas visiškai priklauso ODZ ir yra tokios nelygybės sprendimas. Štai atsakymą gavome: Dabar pabandykime išanalizuoti, ko mums reikia norint sėkmingai išspręsti logaritmines nelygybes? Pirma, sutelkite visą savo dėmesį ir stenkitės nesuklysti atlikdami transformacijas, kurios yra pateiktos šioje nelygybėje. Taip pat reikia atsiminti, kad sprendžiant tokias nelygybes, būtina vengti nelygybės ODZ išsiplėtimų ir susitraukimų, dėl kurių gali būti prarasti ar įgyti pašaliniai sprendimai. Antra, sprendžiant logaritmines nelygybes, reikia išmokti logiškai mąstyti ir suprasti skirtumą tarp sąvokų, tokių kaip nelygybių sistema ir nelygybių rinkinys, kad galėtumėte lengvai pasirinkti nelygybės sprendimus, vadovaudamiesi jos DL. Trečia, norėdami sėkmingai išspręsti tokias nelygybes, kiekvienas iš jūsų turite puikiai žinoti visas elementariųjų funkcijų savybes ir aiškiai suprasti jų reikšmę. Tokios funkcijos apima ne tik logaritmines, bet ir racionaliąsias, galios, trigonometrines ir kt., Žodžiu, visas tas, kurias studijavote mokyklinės algebros metu. Kaip matote, išstudijavus logaritminių nelygybių temą, nėra nieko sudėtingo sprendžiant šias nelygybes, jei esate atsargūs ir atkaklūs siekdami savo tikslų. Norint išvengti problemų sprendžiant nelygybes, reikia kuo daugiau praktikuotis, sprendžiant įvairias užduotis ir tuo pačiu prisiminti pagrindinius tokių nelygybių sprendimo būdus ir jų sistemas. Jei nepavyksta išspręsti logaritminių nelygybių, turėtumėte atidžiai išanalizuoti savo klaidas, kad ateityje prie jų nebegrįžtumėte. Norėdami geriau suprasti temą ir konsoliduoti nagrinėjamą medžiagą, išspręskite šias nelygybes: Logaritmo apibrėžimas Lengviausias būdas tai parašyti matematiškai: Logaritmo apibrėžimą galima parašyti kitu būdu: Atkreipkite dėmesį į apribojimus, taikomus logaritmo pagrindui ( a) ir poblogaritminei išraiškai ( x). Ateityje šios sąlygos pavirs svarbiais OD apribojimais, į kuriuos reikės atsižvelgti sprendžiant bet kokią lygtį su logaritmais. Taigi, dabar, be standartinių sąlygų, lemiančių ODZ apribojimus (reiškinių pozityvumas pagal lyginių galių šaknis, nelygus vardiklis nuliui ir kt.), Taip pat reikia atsižvelgti į šias sąlygas: Atkreipkite dėmesį, kad nei logaritmo bazė, nei sublogaritminė išraiška negali būti lygi nuliui. Taip pat atkreipkite dėmesį, kad pati logaritmo reikšmė gali įgauti visas įmanomas reikšmes, t.y. Logaritmas gali būti teigiamas, neigiamas arba nulis. Logaritmai turi daug skirtingų savybių, kylančių iš galių savybių ir logaritmo apibrėžimo. Išvardinkime juos. Taigi, logaritmų savybės: Produkto logaritmas: Trupmenos logaritmas: Atimant laipsnį iš logaritmo ženklo: Ypatingą dėmesį atkreipkite į tas iš paskutinių išvardytų savybių, kuriose modulio ženklas atsiranda gavus laipsnį. Nepamirškite, kad padėdami lyginę galią už logaritmo ženklo ribų, po logaritmu arba prie pagrindo, turite palikti modulio ženklą. Kitos naudingos logaritmų savybės: Paskutinė savybė labai dažnai naudojama sudėtingose logaritminėse lygtyse ir nelygybėse. Jį reikia prisiminti taip pat, kaip ir visus kitus, nors dažnai pamirštamas. Paprasčiausios logaritminės lygtys atrodo taip: Ir jų sprendimas pateikiamas formule, kuri tiesiogiai išplaukia iš logaritmo apibrėžimo: Kitos paprasčiausios logaritminės lygtys yra tos, kurias naudojant algebrines transformacijas ir aukščiau pateiktas logaritmų formules bei savybes galima redukuoti į formą: Tokių lygčių sprendimas, atsižvelgiant į ODZ, yra toks: Kai kurie kiti logaritmines lygtis su kintamuoju bazėje gali būti sumažintas iki formos: Tokiose logaritminėse lygtyse bendroji sprendinio forma taip pat tiesiogiai išplaukia iš logaritmo apibrėžimo. Tik šiuo atveju yra papildomų DZ apribojimų, į kuriuos reikia atsižvelgti. Dėl to, norėdami išspręsti logaritminę lygtį su kintamuoju bazėje, turite išspręsti šią sistemą: Sprendžiant sudėtingesnes logaritmines lygtis, kurių negalima redukuoti iki vienos iš aukščiau pateiktų lygčių, ji taip pat aktyviai naudojama kintamasis pakeitimo metodas. Kaip įprasta, naudojant šį metodą, reikia atsiminti, kad įvedus pakeitimą lygtis turėtų supaprastėti ir joje nebelikti seno nežinomybės. Taip pat turite nepamiršti atlikti atvirkštinio kintamųjų pakeitimo. Kartais sprendžiant logaritmines lygtis tenka naudoti ir grafinis metodas. Šis metodas susideda iš funkcijų, esančių kairėje ir dešinėje lygties pusėse, grafikus sukonstruojant kuo tiksliau vienoje koordinačių plokštumoje, o tada iš brėžinio surandant jų susikirtimo taškų koordinates. Tokiu būdu gautos šaknys turi būti patikrintos pakeičiant pradinę lygtį. Sprendžiant logaritmines lygtis dažnai taip pat praverčia grupavimo metodas. Naudojant šį metodą, svarbiausia atsiminti, kad: norint, kad kelių veiksnių sandauga būtų lygi nuliui, būtina, kad bent vienas iš jų būtų lygus nuliui, o likusieji egzistavo. Kai veiksniai yra logaritmai arba skliaustai su logaritmais, o ne tik skliaustai su kintamaisiais, kaip racionaliosiose lygtyse, gali atsirasti daug klaidų. Kadangi logaritmai turi daug apribojimų regione, kuriame jie egzistuoja. Sprendžiant logaritminių lygčių sistemos Dažniausiai turite naudoti pakeitimo metodą arba kintamojo pakeitimo metodą. Jei yra tokia galimybė, tada sprendžiant logaritminių lygčių sistemas reikia stengtis, kad kiekviena iš sistemos lygčių būtų individualiai suformuota į tokią formą, kurioje būtų galima pereiti nuo logaritminės lygties prie racionalus. Paprasčiausios logaritminės nelygybės sprendžiamos maždaug taip pat, kaip ir panašios lygtys. Pirma, naudojant algebrines transformacijas ir logaritmų savybes, turime stengtis juos suvesti į tokią formą, kad kairėje ir dešinėje nelygybės pusėse esantys logaritmai turės vienodus pagrindus, t.y. gaukite formos nelygybę: Po to reikia pereiti prie racionalios nelygybės, atsižvelgiant į tai, kad šis perėjimas turėtų būti atliekamas taip: jei logaritmo pagrindas yra didesnis už vieną, tada nelygybės ženklo keisti nereikia, o jei logaritmo bazė yra mažesnė už vieną, tada nelygybės ženklą reikia pakeisti į priešingą (tai reiškia, kad „mažiau“ reikia pakeisti į „daugiau“ arba atvirkščiai). Tokiu atveju nereikia keisti minuso ženklų į pliusus, apeinant anksčiau išmoktas taisykles. Užrašykime matematiškai, ką gauname atlikę tokį perėjimą. Jei bazė yra didesnė už vieną, gauname: Jei logaritmo bazė yra mažesnė už vieną, pakeičiame nelygybės ženklą ir gauname tokią sistemą: Kaip matome, sprendžiant logaritmines nelygybes, kaip įprasta, taip pat atsižvelgiama į ODZ (tai yra trečioji sąlyga aukščiau pateiktose sistemose). Be to, šiuo atveju galima nereikalauti abiejų poaritminių posakių pozityvumo, o reikalauti tik mažesnės iš jų pozityvumo. Sprendžiant logaritminės nelygybės su kintamuoju bazėje logaritmas, reikia savarankiškai apsvarstyti abu variantus (kai bazė yra mažesnė už vieną ir didesnė už vieną) ir sujungti šių atvejų sprendinius į aibę. Kartu reikia nepamiršti ir DL, t.y. apie tai, kad ir pagrindinė, ir visos poblogaritminės išraiškos turi būti teigiamos. Taigi, sprendžiant formos nelygybę: Mes gauname tokį sistemų rinkinį: Sudėtingesnes logaritmines nelygybes taip pat galima išspręsti naudojant kintamųjų pokyčius. Kai kurioms kitoms logaritminėms nelygybėms (pvz., logaritminėms lygtims) išspręsti reikalinga abiejų nelygybės ar lygties pusių logaritmo analizė. Taigi, atliekant tokią procedūrą su logaritminėmis nelygybėmis, yra subtilumo. Atkreipkite dėmesį, kad imant logaritmus į bazę, didesnę už vienetą, nelygybės ženklas nesikeičia, tačiau jei bazė yra mažesnė už vieną, tada nelygybės ženklas apverčiamas. Jei logaritminės nelygybės negalima redukuoti iki racionalios arba išspręsti naudojant pakaitalą, tokiu atveju reikia naudoti apibendrintas intervalų metodas, kuris yra toks: Norint sėkmingai pasiruošti fizikos ir matematikos KT, be kita ko, būtina įvykdyti tris svarbiausias sąlygas: Sėkmingas, kruopštus ir atsakingas šių trijų punktų įgyvendinimas leis jums parodyti puikų KT rezultatą, maksimalų, ką sugebate. Jei manote, kad radote klaidą mokomoji medžiaga, tada prašau parašyti apie tai el. Taip pat galite pranešti apie klaidą socialinis tinklas(). Laiške nurodykite dalyką (fizika ar matematika), temos ar testo pavadinimą arba numerį, uždavinio numerį arba vietą tekste (puslapyje), kur, jūsų nuomone, yra klaida. Taip pat aprašykite, kokia yra įtariama klaida. Jūsų laiškas neliks nepastebėtas, klaida bus arba ištaisyta, arba jums bus paaiškinta, kodėl tai nėra klaida.

Sprendimo pavyzdžiai
![]()



3x > 24;
x > 8. ![]()
Ko reikia logaritminėms nelygybėms išspręsti?
Namų darbai




![]()
![]()

![]()


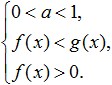

Kaip sėkmingai pasiruošti fizikos ir matematikos KT?
Radai klaidą?





